Triangle rectangle et demi-cercle

1°) Triangle rectangle et demi-cercle

Théorème direct:

"Un triangle rectangle est inscriptible dans un demi-cercle de diamètre son hypoténuse"

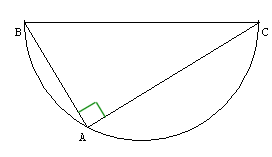
Théorème réciproque:

"Si un triangle est inscriptible dans un demi-cercle de diamètre un de ses côtés, alors il est rectangle"

2°) Triangle rectangle et médiane

Théorème:

"Dans un triangle rectangle, la médiane issue du sommet de l'angle droit est égale à la moitié de l'hypoténuse."

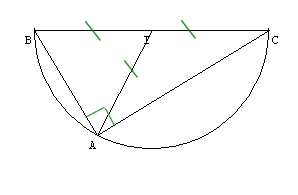
Les segments [IB], [IC], [IA] sont de même longueur, ce sont les rayons du cercle.

Théorème réciproque:

"Si dans un triangle, la médiane issue d'un sommet est égale à la moitié du côté opposé, alors il est rectangle en ce sommet."Remarque: Si ABC est rectangle en A, la médiane issue de A est égale à la moitié de l'hypoténuse.

Exercice : Soit un cercle de centre I et de diamètre [BC] tel que BC = 14cm.

Placez le point A sur ce cercle tel que BA = 8,4cm.

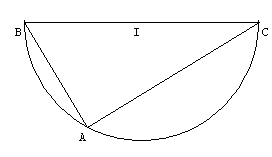
a) Quelle est la nature de ABC?

b) Calculez AC.

c) Calculez l'aire de ABC

 Pour voir la solution complète, cliquez ici.

Exercice supplémentaire (avec l'aimable autorisation de Franck Jarnier)

© J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.