
Théorème de Pythagore:
Théorème direct: "Si un triangle ABC est rectangle en A, alors BC² = AB² + AC²"
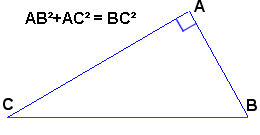
Pour les curieux: une démonstration du théorème de Pythagore
Exemple: Si ABC est rectangle en A et si AB = 4,8cm et AC = 2cm , voyons comment calculer BC.
ABC étant rectangle en A, d'après le théorème de Pythagore: BC² = AB² +AC²
d'où BC² = 4.8² + 2²
BC² = 23.04 + 4 = 27.04
BC
= 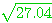 = 5.2
= 5.2
Donc BC = 5,2cm.
Exercice 1:
Un triangle ABC rectangle en A est tel que AB = 5,4cm et AC = 7.2cm. Calculer BC en cm. Veuillez entrer votre réponse :
Exercice 2:
Un triangle DEF est rectangle en E. Sachant que DE = 4,2cm et DF = 7cm, calculer EF en cm. Veuillez entrer votre réponse:
Théorème réciproque: Si un triangle ABC est tel que BC² = AB² + AC², alors ABC est rectangle en A."
Exemple: Soit un triangle IJK tel que IJ = 6cm; IK = 6,3cm et JK = 8,7cm. Quelle est la nature de IJK?
Calculons : IJ² + IK²= 6² + 6.3² = 36 + 39.69 = 75.69
JK² = 8.7² = 75.69
Donc JK² = IJ² + IK². D'après le théorème réciproque de Pythagore, IJK est rectangle en I.
Exercice 3:
Un triangle GHI est tel que GH = 7,5cm; HI = 10cm et GI = 12,5cm. Nature du triangle? Veuillez entrer votre réponse:
© J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.