
Solution du problème:
a) Le triangle ABC est inscrit dans le demi-cercle de rayon [BC].
"Si un triangle est inscriptible dans un demi-cercle de diamètre un de ses côtés, alors il est rectangle"
donc ABC est rectangle en A.
b) Le triangle ABC étant rectangle en A, d'après le théorème de Pythagore:
BC² = AB² + AC²
donc AC² = BC² - AB²
AC² = 14² - 8,4²
AC² = 196 -70,56
AC² = 125,44
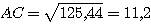
donc AC = 11,2cm
c) Aire d'un triangle rectangle:
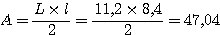
Donc l'aire de ABC est de 47,04cm²