Proportionnalité, pourcentages, échelles

1°) Proportionnalité:

Exemple: on achète 6 roses pour 8,4 €.
Si on n'achète que 3 roses, on ne paiera que 4,2 € (soit, la moitié)
Si on achète 24 roses, on paiera 4 fois plus, c'est-à-dire 33,60 €

On dit alors que le prix des roses est proportionnel au nombre de roses achetées

• Pour connaître le prix de 5 roses on peut procéder par passage à l'unité (c'est-à-dire chercher le prix d'une rose):

1 rose coûte 8,4 : 6 = 1,4 €; donc 5 roses coûteront 5 × 1,4 = 7 €

• On peut aussi travailler dans un tableau de proportionnalité:

On remarque que l'on passe de la première ligne à la seconde en multipliant toujours par 1,4.
On dit que 1,4 est le coefficient de proportionnalité.

Pour calculer le prix de 9 roses, on peut:
- soit utiliser le coefficient:  9 × 1,4 = 12,6 €
- soit additionner entre elles deux colonnes: 6+3 font 9 dans la première ligne, d'où 8,4 + 4,2 = 12,6 € , le prix de 9 roses!

Pour calculer le prix de 10 roses, on peut:
- soit utiliser le coefficient: 10 × 1,4 = 14 €
- soit multiplier la colonne "5" par 2 : en effet 2 × 5 roses font 10 roses et 2 × 7 e font 14 € !

En proportionnalité, il y a donc souvent plusieurs moyens pour trouver la solution.

2°) Pourcentages:

- Un pourcentage est une fraction dont le dénominateur est égal à 100.

Exemple: 3% représente 3/100
Ainsi, prendre 3% de 120 € revient à prendre 3/100 de 120 €
cela fait:  3 × 120 : 100 = 360 : 100 = 3,6 €.

- De même, si on dispose d'une réduction de 6% sur divers articles de 250 €; 300 € et 420 €, on peut calculer le montant de la remise:
  6% de 250 € =  6 ×250 : 100 = 15 € ; 6% de 300 = 6 × 300 : 100 = 18 €; 6% de 450 €= 6 × 450 : 100 = 27 €.

 On peut disposer alors ces résultats sous forme d'un tableau de proportionnalité:

On dit que la première ligne du tableau et la seconde ligne sont proportionnelles.

On passe de la première ligne à la seconde en multipliant toujours par un même coefficient appelé coefficient de proportionnalité.
Ce coefficient se calcule en effectuant 6 : 100 ou 15 : 250 ou 18 : 300 ou encore 27 : 450. Il vaut donc ici 0,06.

 Exemple d'exercice: un article d'une valeur de 310 € est vendu avec une remise de 8% pour la braderie. Calculez son prix définitif.

    - montant de la réduction:  8% de 310 = 8 × 310 : 100 = 24,80 €
    - prix définitif: 310 - 24,80 = 285,20 €

 3°) Échelles:

 Une échelle est donc une fraction qui, lorsqu'il s'agit d'une réduction, s'écrira en général sous la forme 1/....... (numérateur = 1)

Par exemple; le plan d'un ville au 1/10 000 veut dire que les dimensions sur le plan sont dix-mille fois plus petites qu'en réalité.

Chercher quelle distance réelle est représentée sur un tel plan, par un segment de 9cm?
Ou encore, chercher combien mesurera sur ce plan une route 3 km?

On peut, là encore, utiliser un tableau pour récapituler ces données:

On a ici un coefficient de proportionnalité égal à 10 000.
Donc 9cm sur le plan représentent en réalité: 9 × 10 000 = 90 000cm = 900 m
3 km font 300 000cm soit sur le plan 300 000: 10 000 = 30 cm.
 La route de 3km sera donc représentée par un tracé de 30 cm sur le plan.

  Exemple de calcul d'une échelle:

 Sur un plan, une maison de 12m de large ne fait plus que 6cm de large. Quelle est l'échelle du dessin?

On utilise la formule:  

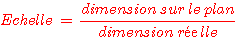
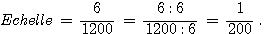
Exemple d'agrandissement:

3°) Exercices:

 a) Une bouteille de bain moussant en promotion contient 1,5 L plus 8% de produit gratuit en supplément.
Calculez la contenance totale de cette bouteille.

 Réponse:

  b) Pour les soldes, un radio-réveil  de valeur 80 € est vendu avec une réduction de 9% . Calculez son prix réel.

Réponse:

 c) Sur un plan au 1/1 000 000 on représente une route de 55 km. Quelle est la longueur, en cm, sur le plan de cette route?

Réponse:

d) Sur le même plan, on veut mesurer un trajet de 14cm. Quelle sera la distance réelle à parcourir (en km )?

Réponse:

 © J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.