Numération

NUMERATION

1°) Ecriture

Il existe plusieurs sortes de numération.

La numération égyptienne


unité	dizaine	centaine	millier	dizaine de mille	centainede mille	million

La numération romaine

I	V	X	L	C	D	M
un	cinq	dix	cinquante	cent	cinq cents	mille

Notre numération

Un nombre peut s'écrire en chiffres ou en lettres.

Il n'y a que dix chiffres : 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Avec ces dix chiffres, on peut écrire une infinité de nombres

Pour écrire les nombres en lettres, on a besoin de savoir orthographier correctement les nombres suivants:

zéro, un, deux, trois, quatre, cinq, six, sept, huit, neuf, dix, onze, douze, treize, quatorze, quinze, seize, vingt, trente, quarante, cinquante, soixante, cent, mille, million, milliard...

Remarques:

cent prend un "s" au pluriel s'il n'est pas suivi d'autre chose ( on écrit trois cents; par contre on écrira deux cent quatre)

mille ne prend jamais "s"

2°) Fractions décimales

Le nombre 3 unités 6 dixièmes 2 centièmes peut s'écrire:

Un nombre décimal peut s'écrire avec la somme d'un nombre entier et de fractions décimales ou avec une seule fraction décimale.

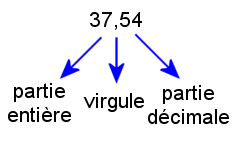
Il peut aussi s'écrire à l'aide d'une écriture décimale (ou à virgule):

3°) Nombres entiers et décimaux

0; 1; 2; 3; 4; 5 ... sont des entiers naturels; ils s'écrivent sans virgule et n'ont pas de partie décimale.

2,4; 0,03; 6,7 ; 5 ; 0; 1,24 sont des nombres décimaux

Remarque: tout nombre entier peut être considéré comme étant aussi décimal (avec une partie décimale nulle)

Pour l'écriture des nombres décimaux, on peut s'aider d'un tableau:

Ainsi, les nombres placés dans le tableau ci-dessous sont respectivement:

27, 08 : vingt sept unités et huit centièmes

30 063,003 5: trente mille soixante trois unités et trente cinq dix-millièmes.

dizaine de mille	mille	centaine	dizaine	unité	dixième	centième	millième	dix-millième
			2	7,	0	8
3	0	0	6	3,	0	0	3	5

4°) Comparaison et valeur approchée:

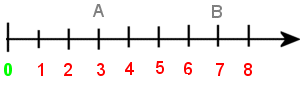
a) abscisse

Sur une demi-droite graduée, un point est repéré par un nombre appelé son abscisse.

Par exemple, le point A est repéré par 3. On dit que l'abscisse de A est 3

B a pour abscisse 7

b) comparaison

Pour comparer deux nombres décimaux, on compare d'abord leurs parties entières.

Ensuite, on compare éventuellement leurs parties décimales en commençant par les dixièmes, puis les centièmes, etc.

Le symbole < veut dire "inférieur" ou "plus petit que"
Le symbole > veut dire "supérieur" ou "plus grand que"

Ranger dans l'ordre croissant signifie: "ranger du plus petit au plus grand"
Ranger dans l'ordre décroissant signifie "ranger du plus grand au plus petit"

Exemple: ranger dans l'rodre croisssant les nombres: 0,8 ; 1 ; 0,26 ; 0,2 ; 0,7 ; 0,3 ; 1,3 ; 0,68 ; 0,19

Cela donne: 0,19 < 0,2 < 0,26 < 0,3 < 0,68 < 0,7 < 0,8 < 1 < 1,3

c) valeurs approchées:

Exemple: 5,72. 5,7 ‹ 5,72 ‹ 5,8

5,7 est la valeur approchée au dixième par défaut de 5,72, on dit aussi que c'est une troncature.
5,8 est la valeur approchée au dixième par excès de 5,72

La valeur approchée la plus proche est ici 5,7, on dit que c'est un arrondi de 5,72.

5°)Exercices:

a) Le chiffre des centièmes de 145,216 est...

Réponse:

b) Le plus petit entier supérieur à 17,8 est...

Réponse:

c) Le plus grand entier inférieur 15,4

Réponse:

d) Nombre mystérieux: trouver le nombre de 5 chiffres dont le chiffre des centaines et le chiffre des centièmes est 6, le chiffre des dixièmes ainsi que celui des dizaines est 4 et tel que le chiffre des unités est 2.

Réponse:

Exercices de comparaison (avec l'aimable autorisation deFranck Jarnier)