Prismes droits

1°) Définition:

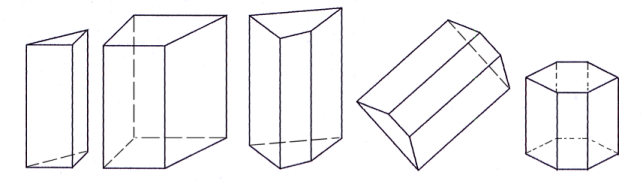
 Les figures ci-dessus sont des prismes droits.
Les faces non-rectangulaires sont les bases. Elles sont parallèles et superposables.
Les faces rectangulaires sont appelées faces latérales. Ce sont des rectangles.

2°) Patron, aire latérale et volume.

La figure ci-dessous est un prisme droit de base un triangle.

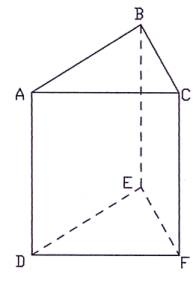
ABC et DEF sont les bases.
Les faces latérales sont les rectangles ACFD, ABED et BCFE.
L'aire latérale est égale à la somme des aires de ces 3 rectangles.
Si on nomme H la hauteur du prisme, cela fait: DE × H + DF × H + EF × H = ( DE + DF + EF ) × H .
Aire latérale = Périmètre de la base × Hauteur.

Le volume est égal au produit de l'aire B de la base (ici aire d'un triangle) multipliée par la hauteur H. 
Volume = Aire de la base × Hauteur.

Exemple: un prisme a pour base un triangle rectangle de dimensions L=8cm; l = 5cm et de hauteur 4cm.
Son volume: V = B × H = ( 8 × 5 : 2 ) × 4 = 80 cm³ .

Exemples de patron:

[ voir l'animation ]

3°) Exercices:

1°) Un prisme a pour base un triangle de base b = 7cm, et hauteur h = 4cm. La hauteur du prisme est de 5cm. Quel est son volume?

Réponse:

 2°)a) Un prisme a pour base un triangle rectangle de dimensions L = 4cm et l = 3cm. Sa hauteur H est de 6cm. Quel est son volume?

Réponse:

b) On sait que l'hypoténuse de la base du prisme précédent fait 5cm. Calculer l'aire latérale.

Réponse:

c) Calculer l'aire totale de ce prisme.

 Réponse:

© J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.