STATISTIQUES

1°) Définitions et graphiques:

  On représente les données statistiques sous forme de tableaux et de graphiques.
Parmi les graphiques, on distingue les "diagrammes en bâtons", les histogrammes et les diagrammes circulaires ou semi-circulaires.

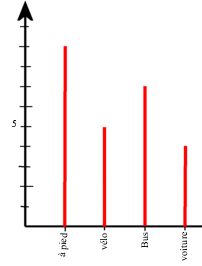
Exemple1: on répartit les élèves d'une classe de 25 élèves selon leur moyen de locomotion pour venir au collège.

Pour la représentation graphique on choisira un diagramme en bâtons car les valeurs des réponses sont isolées.
Le nombre d'élèves correspondant à une catégorie se nomme l'effectif.

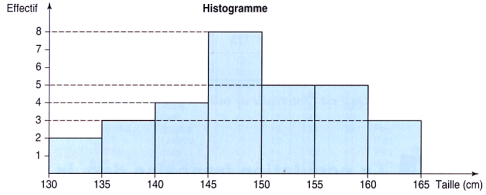
Exemple 2: on répartit les 30 élèves d'une classe selon leur taille. Pour la représentation graphique on utilise un histogramme.

2°) Fréquences et angles.

 La fréquence est le rapport entre un effectif et l'effectif total.
Ainsi, pour le tableau précédent, la fréquence pour la tranche de 135 à 140 est de 3/30 = 1/10 = 0,1.
Dans la pratique, on exprime souvent la fréquence en pourcentage.
Pour calculer un pourcentage, on peut utiliser une formule ou faire un tableau de proportionnalité.

Dans l'exemple précédent, on obtient:

Donc la fréquence = 3 × 100 : 30 = 10. D'où une fréquence de 10%.

On obtient le même calcul avec la formule:

Enfin, pour utiliser un diagramme circulaire, il faut calculer les angles représentants chaque tranche.
Comme l'angle total est de 360°, il suffit d'appliquer le pourcentage (fréquence) à 360.
Par exemple,  si la fréquence est de 10%, on calcule 10% de 360 = 36°; d'où un angle de 36°.
On arrondit souvent le pourcentage et l'angle à l'unité.

Tableau avec les fréquences et les angles (on ajoute une colonne "total" pour simplifier les calculs).

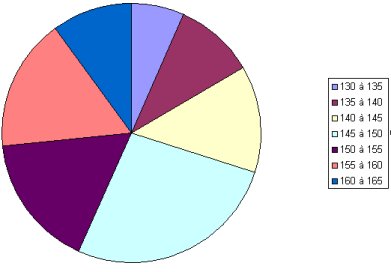
On en déduit le diagramme circulaire:

3°) Exercice:

Compléter le tableau ci-dessous. (Remarque: on arrondira la dernière valeur des angles par défaut pour que le total fasse bien 360°)

© J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.