SUITES D'OPERATIONS

a) Propriétés de l'addition:

• On peut permuter deux termes d'une addition :    a + b = b + a

           18 + 54 = 54 + 18 ; on dit que l'addition est commutative

• Dans une suite d'additions, on peut regrouper des termes à l'aide de parenthèses: ( a  + b ) + c = a + ( b + c )

             ( 12 + 27 ) + 9 = 39 + 9 = 48

              12 + ( 27 + 9 ) = 12 + 36 = 48    ;     donc ( 12 + 27 ) + 9 = 12 + ( 27 + 9 )

 Dans la pratique, on utilise conjointement ces deux propriétés pour calculer des suites d'additions à l'aide de groupements astucieux.

Exemples:  25 + 37 + 42 + 18 + 15 + 13 = ( 25 + 15 ) + ( 42 + 18 ) + (37 + 13)

                                                                  =     40 + 60 + 50 = 150

                    7,3 + 2,5 + 2,9 + 1,7 + 0,5 = ( 7,3 + 1,7 ) + ( 2,5 + 0,5) + 2,9 =

                                                               = 9 + 3 + 2,9 = 14,9

Exemple: 13;7 +5,8 + 4,5 + 2,2 + 4,3 +2,5 = (13,7 + 4,3) + (5,8 + 2,2) + (4,5 + 2,5)

                                                             =        18       +    8          + 7  =  33

 De même, pour simplifier les calculs, on peut grouper des facteurs intéressants dans une suite de multiplications.

Exemple: 125 × 5 × 25 × 3,8972 × 2 × 4 × 8 =  ( 125 × 8 ) × ( 25 × 4) × (5 × 2) × 3,8972

                                                                = 1000 × 100 × 10 × 3,8972 = 3 897 200

Remarque: il peut être utile de grouper 5 avec 2 ; 4 avec 25 et 8 avec 125.

Exercice: Calculer astucieusement: 8 × 4,36 × 1,25 × 2,5 × 4

 Réponse:

 2°) Règles de priorités:

a) avec parenthèses:

Il y a priorité aux parenthèses, puis aux crochets, etc.

Exemples:  137 - ( 89 - 36 ) = 137 - 53 = 84.

                    25 × [ 22 - (14 - 6 ) ] = 25 × [ 22 - 8 ] = 25 × 4 = 100

Exercice: Calculez : 136 - [ 6 × ( 15 - 7 ) ]

Réponse:

b) sans parenthèses:

En absence de parenthèses, de multiplications et de divisions, on effectue les calculs dans l'ordre, en commençant par les deux premiers termes...

Exemple:  29 + 17 - 15 + 9 - 6 =

                      46   - 15 + 9 - 6 =

                             31   + 9 - 6 =

                                   40  - 6  =

                                        34

En absence de parenthèses, les multiplications et les divisions sont prioritaires.

Exemple: 59 - 5 × 8 = 59 - 40 = 19   ( et non pas 54 - 8 = 46. On peut en particulier vérifier par ce type de calculs si on possède une calculatrice scientifique ou non... Si on tape sur une calculette Scientifique 59 - 5 ×8, elle doit afficher 19; par contre, une calculette "ordinaire" donnera pour résultat 46 car ce type de calculette calcule d'abord 59 - 5 sans tenir compte de la priorité des opérations )

 De même: 18 - 49 : 7 = 18 - 7 = 11

Exercice: Calculez : 138 - 8 × 12

Réponse:

3°) Distributivité :

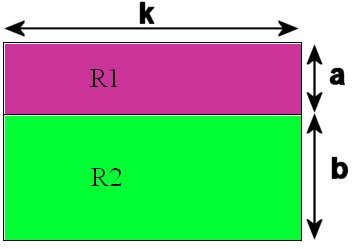
Le rectangle ci-dessous est constitué de deux parcelles R1 et R2. Calculons de deux façons différentes l'aire totale de ce rectangle:

1ère méthode: la largeur totale du rectangle est a+b; sa longueur est k.

l'aire du rectangle s'obtient en faisant longueur × largeur, soit: k × (a + b).

2ème méthode: on calcule d'abord l'aire du rectangle R1 :         A1 = k × a

                              puis on calcule l'aire du rectangle R2:           A2 = k × b

Enfin on additionne les deux aires A1 et A2, ce qui donne: (k × a) + (k × b).

Conclusion: k × ( a + b ) = ( k × a ) + ( k × b ).

Cette formule illustre une propriété appelée DISTRIBUTIVITE. On dit que la multiplication est distributive par rapport à l'addition et la soustraction.

Remarques:  - le signe × n'est pas obligatoire ainsi que les parenthèses autour de k×a et k×b.

                       - la formule s'applique aussi bien avec l'addition que la multiplication.

Ce qui donne:  

Applications: Cette formule permet de calculer de deux façons différentes, d'aider pour le calcul mental, de simplifier des expressions algébriques.

Exemples:  - Calculer de deux façons différentes :   A = 15 ( 18 - 7 )

1ère méthode : A = 15 × 11 = 165   ; 2ème méthode: A = 15 × 18 - 15 × 7 = 270 - 105 = 165.

                 - Calculer "mentalement"  B = 36 × 999  

B = 36 × 999 = 36 × ( 1000 -1 ) = 36 × 1000 - 36 × 1 = 36000 - 36 = 35 964

4°) Notations simplifiées

• Le signe × peut être omis s'il n'y a pas d'ambiguïté possible ( par exemple entre des lettres ou devant des parenthèses)

          Ainsi:  a × b = ab   ; 5 × a = 5a ;  6 × ( 19 + 25 ) = 6 ( 19 + 25 )

• On n'écrit pas : a × a = aa; on écrit a × a = a² ; qui se lit " a au carré" ou encore "a puissance 2"

          de même, a × a × a = a³ ; etc.

• a + a + a = 3 × a = 3a ; a + a = 2a ; a + a + a + a = 4a ; etc.

            Attention de ne pas confondre  a + a + a = 3a   et a × a × a = a³

• La distributivité permet de simplifier des expressions algébriques (expressions contenant des lettres remplaçant des nombres)

          Exemple 1: simplifiez  C = 7 ( a + 5 ) = 7a + 7×5 = 7a + 35 .

          Exemple 2: simplifiez D = 6 ( a + 8) + 5 ( a - 4 ) = 6a + 48 + 5a - 20 = 11a + 28

Ces notions seront vues en détail en classe de quatrième ...

 Exercice ( pour les champions!): Simplifiez E = 9 ( a + 6 ) + 3 ( 7 - 3a )

         Réponse:

 © J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.