1°) Généralités :

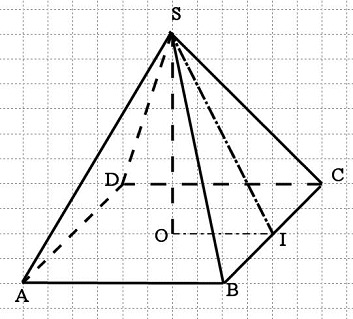
·         ABCD est la  base

·         S est le  sommet.

·         Soit O le centre de symétrie de la base ABCD.

·         La longueur  SO représente la hauteur de la pyramide.

·         Les triangles ABS ; BCS ; CDS et ADS sont les faces latérales .

·         L’aire latérale est la somme des aires de ces 4 triangles .

·         Les segments [SA] ; [SB] ; [SC] ;[SD] sont des arêtes.

·         Soit I le milieu de [BC].

·         Le segment [SI] est la hauteur du triangle SBC ;

       on l’appelle l’apothème.  de la pyramide.

2°) Volume :

Le volume d’une pyramide s’obtient par la formule :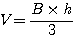     

où  B représente l’aire de la base.

 

Exemple : une pyramide de base carrée de côté c = 6cm et de hauteur H = 4cm a pour volume :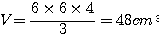

 3°) Calcul de l’apothème, de l’aire latérale :

On utilise le théorème de Pythagore dans le triangle SOI.

SI² =  SO² + OI²  =   4² + 3² = 16 + 9 = 25

SI =

Aire latérale :  A = 4 ´ aire d’un triangle

                           =

 

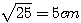
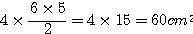
4°) Exercices :

a)      Une pyramide a pour base un carré de 5m de côté et une hauteur de 9m. calculer son volume.

 

b)      Une pyramide a pour base un carré de 12cm de côté et une hauteur de 8cm.

Calculer son volume

son apothème

puis son aire latérale.