Proportionnalité, vitesse...

 1°) Proportionnalité

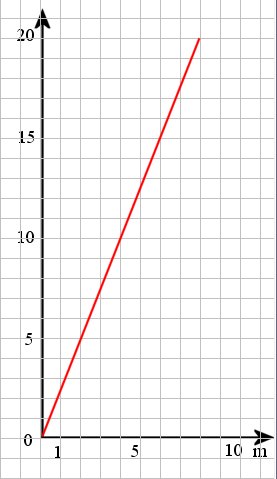
Un tissu est vendu à 2,50 € le mètre. Le prix est proportionnel à la longueur du tissu. On peut utiliser un tableau de proportionnalité.

Le coefficient de proportionnalité est 2,5. On passe de la première ligne à la seconde en multipliant par 2,5.

La représentation graphique est une droite qui passe par l'origine.

2°) "Produits en croix"

Pour trouver une valeur manquante (quatrième proportionnelle) dans un tableau de proportionnalité, on peut utiliser les "produits en croix".

Exemple: on achète six bouteilles d'eau pour 1,44 €, quel est le prix de 5 bouteilles?

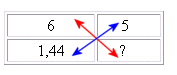
Soit x le prix des 5 bouteilles,  6x = 4 × 1,44..
donc x =: 5 × 1,44 : 6 = 1,2
Le prix de 5 bouteilles est donc de 1,20 €.

2°) Pourcentages:

- Un pourcentage est une fraction dont le dénominateur est égal à 100.

Exemple: 3% représente 3/100
Ainsi, si un article valant 120 € est vendu avec une réduction de 3% , le montant de cette réduction est de  3 × 120 : 100 = 360 : 100 = 3,6 €.
Il coûtera alors:  120 - 3,6 = 116,40 € .

- Un pourcentage est un cas particulier de proportionnalité.
Pour trouver un pourcentage, on peut donc faire un tableau de proportionnalité.

Exemple: Une montre valant 135 € est vendue 102,60 € après réduction pour les soldes. Calculer le pourcentage de cette réduction.

Montant de la réduction : 135 - 102,60 = 32,40 €

On calcule la quatrième proportionnelle par un produit en croix :   (32,40 × 100 ) : 135 = 24
Le pourcentage de la réduction est donc de 24%.

4°) Vitesse moyenne:

La vitesse moyenne d'un mobile est le quotient de la distance d parcourue le temps t du parcours.

 Pour calculer une distance :  d = v × t

Pour calculer une durée : t = d : v

Exemple1: une voiture parcourt 120 km en 2h; sa vitesse est v = d:: t = 120 : 2 = 60 km./h

Exemple 2 : Un cycliste roule pendant 3 minutes à la vitesse de 13m/s..  3min = 3 × 60 = 180 s
La distance parcourue est d = v × t =: 13 × 180 = 2340 m = 2,43 km.

5°) Changement d'unité:

exemple 1: un véhicule se déplace à la vitesse de 25,2 km/h; exprimez cette vitesse en m/s.

En 1h, il parcourt 25,2 km = 25200m. 1h = 3600s.
En 1 seconde, il parcourt:  25200:3600 = 7
Sa vitesse est donc de 7m/s.

Autre façon de présenter cette conversion:

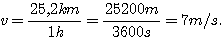
exemple 2 : une voiture roule pendant 2h12min à la vitesse moyenne de 65km/h. Quelle distance a-t-elle parcouru?

Il faut convertir la durée en "heures décimales": 2h12min = 2h + 12min = 2h + 12/60 h = 2 + 0,2 = 2,2h.
d = v × t = 65 × 2,2 = 143 km.

exemple 3: Jan Ullrich a gagné le tour de France en 1997. il a parcouru au total 3944km à la vitesse moyenne de 39,24km/h.
Calculez le temps qu'il a mis pour effectuer ce parcours (arrondir à la minute).

t = d/v = 3944 : 39,24. On a affaire à une division horaire...

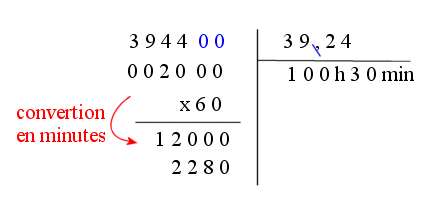
Le temps mis est de 100h 30 min !

3°) Exercices:

a) Le martinet d'Asie parcourt 1,35km en 30s. Calculez sa vitesse en m/s.

b) Un cycliste roule à la vitesse de 9m/s. Calculez sa vitesse en km/h.

c) La vitesse du son est d'environ 300m/s. Calculer la distance en km parcourue en 2minutes.

 © J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.