LES FONCTIONS

1°) Notion de fonction

Une fonction est un processus qui transforme un nombre de départ appelé antécédent en un nombre d'arrivée appelé image.

On peut comparer ce processus à une "machine" à transformer des nombres:

Exemple 1 : on considère la fonction f  "élever au carré" qui à tout nombre x fait correspondre son carré f(x) = x²

on peut tracer la courbe représentative de cette fonction:

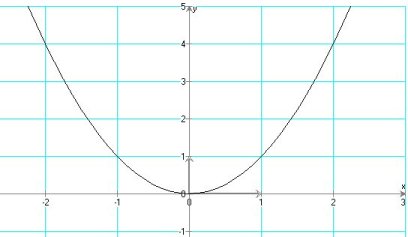
Exemple 2: Plus généralement, on dira qu'une fonction g est définie par sa "formule" par exemple g(x) = sin x ,
ou par un tableau de valeurs, ou encore par sa représentation graphique...

 Tableau de valeurs:

Représentation graphique:

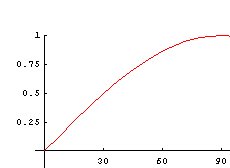
2°) Fonction linéaire.

Une fonction est dite linéaire lorsque son expression est de la forme  f(x) = a x où a est le coefficent constant.

f(-1,5) = -3,75  on dit que -1,5 est l'antécédent de -3,75

f(4) = 10; on dit que 10 est l'image de 4.

Une fonction linéaire correspond à une situation de proportionnalité.

La représentation graphique est une droite passant par l'origine du repère.

Exemples d'exercices:

Ex1 : on considère le fonction f(x) = 0,4 x.

a) trouvez l'image de 3  :   f(3) = 0,4 × 3 = 1,2
b) trouvez l'antécédent de 3,6: f(x) = 0,4 x = 3,6
on résout l'équation 0,4 x = 3,6 ;  x = 3,6 : 0,4 = 9

Ex 2 : g est une fonction linéaire telle que l'image de 7 soit 64,4. Trouvez l'expression littérale de g(x).
g étant linéaire on a g(x) = ax; donc g(7) = a × 7 = 64,4; d'où a = 64,4 : 7 = 9,2.
Donc g(x) = 9,2 x.

3°) Fonction affine

Une fonction f est affine si son expression est du type: f(x) = a x + b

Exemple: f(x) = 2x -3

La représentation d'une fonction affine est une droite passant par le point de coordonnées (0 ; b).
Cette droite est parallèle à la représentation graphique de la fonction linéaire x -> ax .

Cas particuliers:

• si a = 0 :  x -> b est une fonction constante; sa représentation est une droite parallèle à l'axe (Ox)
• si b = 0:  on retrouve le cas d'une fonction linéaire qui est un cas particulier de fonction affine.

Proportionnalité des accroissements:

   Les accroissements de x et de f(x) sont proportionnels, ce qui signifie que :

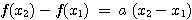  a est le coefficent de proportionnalité

Exercices:

Ex 1 :         f(x) = 5x -8 .
a) Trouvez l'image de -4  :   f(-4) = 5 × (-4) - 8 = -20 -8 = -28
b) Trouvez l'antécédent de 7 :  f(x) = 5 x - 8 = 7 ; on résout l'équation
     5x = 8 + 7 = 15 ;  x = 15 : 5 = 3 . L'antécédent de 7 est 3.

Ex 2 : La fonction affine g est telle que g(4 ) = -4 et  que g(0) = 8. Trouvez l'expression de g.
      g(x) de la forme: g(x) = ax +b or g(0) = 8 ; donc b = 8
      g(x) = ax + 8  d'où g(4 ) = 4 a + 8 = -4 ;  donc 4a = -4 - 8 = -12 et a = -12 : 4 = -3.
      Conclusion:  g(x) = -3x + 8

4°) Exercices

a) Calculer l'image de 9 par f(x) = 6x

b) Calculer l'antécédent de 21 par f(x) = 6x  

c) Calculer l'image de 19 par g(x) = 7x - 13

d) Calculer l'antécédent de 43 par g(x) = 7x - 13