Corrigé contrôle commun 4e janvier 2005

CORRIGE CONTROLE COMMUN
classe de4ème
JANVIER 2005

Activités numériques:

Ex1 (1point):

        A = 12 - 3 ×(-4) + 7 × (3-3-11) - 12 × 5
            = 12 + 12 + 7 × (-12) - 60
            = 12 + 12 - 84 - 60 = -120

Ex2 (2 points):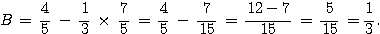

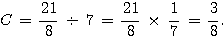
Ex 3 (2 points):

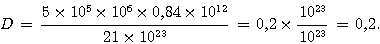
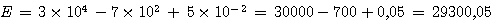
Ex4 (1 point):

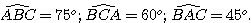
Ex5 (5 points):

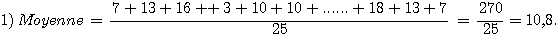
2) Tableau 1:

N: Note	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Effectif	0	0	1	0	4	0	6	0	0	3	0	0	4	0	0	2	0	4	1	0
Fréquence %	0	0	4	0	16	0	24	0	0	12	0	0	16	0	0	8	0	16	4	0

Tableau 2:

N: Note
Effectif	1	10	3	4	7
Eff. cum.	1	11	14	18	25

Histogramme:

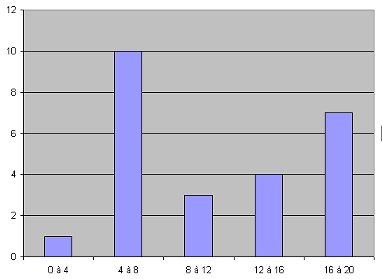
Moyenne à partir du tableau:

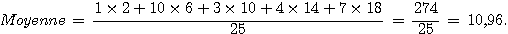
Activité géométriques:

Ex1 (2,5 points):

1°) Le triangle ABD est rectangle en A. D'après le théorème de Pythagore:

BD² = AD² + AB² = 3² + 4² = 25

2°) BD = DC = 5cm. Donc BDC est isocèle.

Ex2 (3 points):

Calculons: IJ² = 5,1² = 26,01
JK² = 2,4² = 5,76
KI² = 4,5² = 20,25

or: 20,25 + 5,76 = 26,01; donc JK² + KI² = IJ²

D'après le théorème réciproque de Pythagore, IJK est donc rectangle en K.

Ex3 (4 points):

1°) "La droite qui joint les milieux de deux côtés d'un triangle est parallèle au troisième côté".
I milieu de [FG] et J milieu de [EG]; donc (IJ) // (EF).

2°) "La parallèle à un côté d'un triangle, menée par le milieu d'un deuxième côté, coupe le troisième en son milieu".
J milieu de [EG] et (JK) // (EH); donc K milieu de [HG]

3°) I milieu de [FG] et K milieu de [HG]; même théorème qu'au 1°)
donc (IK) // (FH).

Ex4 (2,5 points):

ABC est rectangle en B; d'après le théorème de Pythagore:

   AC² = AB² + BC²; donc BC² = AC² - AB²
   BC² = 7² - 6,5² = 6,75.

Donc l'échelle doit être placée à 2,6m du mur.

Problème:

1°) "Si un triangle est inscrit dans un demi-cercle de diamètre un de ses côtés, alors il est rectangle"
donc ABD est rectangle en B.
(1point)

2°) Théorème de Pythagore dans ABC:
BD² = AD² - AB² = 10² - 5² = 75.

(2 points)

3°) OA = OB = rayon = 5cm et AB = 5cm; donc AOB est équilatéral.
(1 point)

4°) B est milieu de [AE] car E symétrique de A par rapport à B et O est milieu de [AD] car O centre du cercle de diamètre [AD].
D'après le théorème des milieux (voir AG 3°)), (OB) // (ED).
(1,5 points)

" La longueur du segment qui joint les milieux de deux côtés d'un triangle est égal à la moitié du troisième côté".
Donc ED = 2 × OB = 2 × 5 = 10cm.
(1,5 points)

5°) F est un point du cercle de diamètre [AD] donc:

ABDF est un rectangle car il a 3 angles droits.
(1 point)

6°) OA = OF = rayon; donc O équidistant de A et de F.
Donc O appartient à la médiatrice de [AF].
(1 point)

Figure sur 3 points

Il reste 4 points pour la présentation et la rédaction.