CORRECTION

DEVOIR COMMUN N°2 de 4ème

Activités numériques (18 points)

Exercice 1

Exercice 2 :

a ) C = 2 ( 3x – 4 ) + 5 ( x + 1 ) = 6x – 8 + 5x +5 = 11x - 3

b) Pour x = 0, C = 11 × 0 – 3 = -3

Exercice 3 :

a ) D = ( 4x – 7 ) ( x + 2 ) = 4x² + 8x – 7x – 14 = 4x² +x - 14

b) Pour x = -2, D = [4×(-2)] ( -2+2) = 0

Exercice 4 :

Exercice 5 :

a) 149 597 870,691 km = 1,495 958 706 91 × 10⁸ km

b) 0,000 000 000 015 mm = 1,5 × 10^{-11 mm}

c) 22 millions = 2,2 × 10⁷

Exercice 6 :

a) 2x + 6 = 7

2x = 7 – 6

2x = 1

x = 1 :2

x = 0,5

b) 3x – 12 = 5x + 7

-12 – 7 = 5x – 3x

-19 = 2x

Donc x = -19 : 2

x = -9,5

c)

Exercice 7 :

a) P = 8 × 2 + 7 × 2 = 16 + 14 = 30

b) 2x+4 = x+5

2x – x = 5 – 4

x = 1

Exercice 8 : Caroline a deux fois l’âge de Zoé moins cinq ans. Zoé a la moitié de l’âge de Pierre.
Si on additionne les âges de Pierre, Caroline et Zoé, on obtient 25 ans. Soit x l’âge de Zoé.

a) Age de Caroline : 2x -5

b) Age de Pierre : 2x

c) Equation : x + 2x + 2x -5 = 25

5x – 5 = 25

5x = 25 + 5

5x = 30

x = 30 : 5

x = 6

d) Age de Zoé : 6ans ; âge de Caroline : 2×6-5= 12-5 = 7 ans ; âge de Pierre : 2×6 = 12ans

Activités géométriques (18 points)

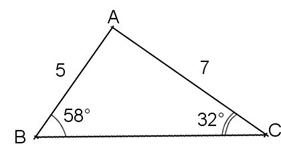
Exercice 1 : a) Comme la somme des angles d’un triangle fait 90°, il vient que  = 90° donc ABC est rectangle en A. b) D’après le théorème de Pythagore dans le triangle ABC rectangle en A : BC² = AB² + AC² = 5² + 7² = 25 + 49 = 74 c)

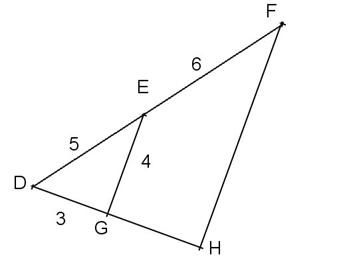
Exercice 2 : Pour la figure suivante, on sait que (EG) est parallèle à (FH) et que DG = 3cm ;
DE = 5cm ; GE = 4cm ; EF = 6cm.:

a) Dans le triangle DFH on sait que E appartient à [DF], que G appartient à [DH] et que les droites (EG) et (FH) sont parallèles. D’après le théorème de Thalès :

b) Périmètre du trapèze EFHG = 4+6+8,8+3,6 = 22,4cm

c) Calculons :

DE² = 5² = 25

DG² + EG² = 3² + 4² = 9 + 16 = 25

On remarque que DE² = DG² + EG²

D’après le théorème réciproque de Pythagore, DEG est rectangle en G

d) DEG étant rectangle en G, les droites (DG) et (EG) sont perpendiculaires.

De plus, les droites (EG) et (FH) sont parallèles par hypothèse.

« Si deux droites sont parallèles, toute perpendiculaire à l’une est perpendiculaire à l’autre »

Donc (DH) et (FH) sont perpendiculaires ; il en résulte que DHF est rectangle en H.

Exercice 3:

a) Patron :

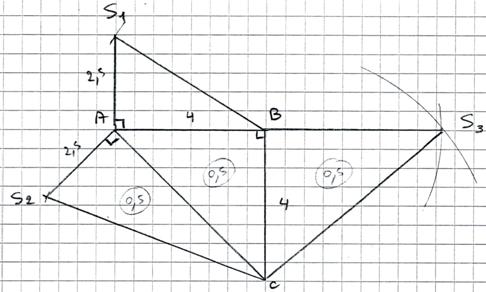
b) D’après le théorème de Pythagore dans SAB étant rectangle en A :

SB² = SA² + AB² = 2,5² + 4² = 6,25 + 16 = 22,25

Exercice 4 :

a) Réduction du triangle CIT de coefficient 0,8 : 7 ×0,8 = 5,6cm ; 10 × 0,8 = 8cm.

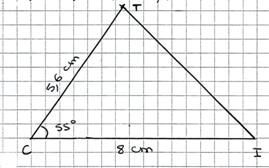
b) Coefficient d’agrandissement :

15 : 4 = 3,75

Le coefficient d’agrandissement est de 3,75.