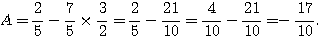
CORRECTION
du Devoir
Commun de Mathématiques de 4ème
mai 2005
ACTIVITES NUMERIQUES ( 12 points )
Exercice n°1 : Calculer, en faisant apparaître les étapes intermédiaires et en donnant le résultat sous forme fractionnaire ( simplifiée ) :
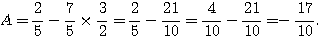
Exercice n°2 : Calculer et donner l’écriture scientifique de B et de C:
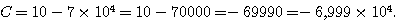
Exercice n°3 : Supprimer les parenthèses puis réduire l’expression :
D = ( 2a + 5b - 3c ) - ( -2a + b -9c ) = 2a+5b-3c+2a-b+9c = 4a + 4b + 6c .
Exercice n°4 :
1) Résoudre l’équation suivante : 6- x = 2x
6 = 2x + x =>
6 = 3x => x = 6:3 = 2. Donc x = 2.
2) Résoudre l’équation suivante : 3x + 7 = 2x - 3
3x
- 2x = - 3 - 7 => x = -10. Donc x = -10 .
Exercice n°5 : Développer et réduire E , F et G :
E = 5 ( x – 6 )
= 5x - 30 .
F = ( 3x+ 4 ) ( 2x + 5 )
= 6x² + 15x + 8x + 20 = 6x² + 23x + 20 .
G = ( 3x – 5 ) ( 4 – 2x )
= 12x - 6x² - 20 + 10x = -6x² + 22x -20 .
Calculer F pour x = - 1
: F = 6 × (-1)² + 23 × (-1) + 20 = 6 - 23 + 20 = 3 .
Exercice n°6 :
Il
paraît que le nombre 371 est égal à la somme des cubes de chacun de ses
chiffres.
Est-ce
exact ? Justifier votre réponse par un calcul .
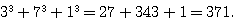
Donc c'est vrai !
Exercice n°7 :
Sachant
qu'un oiseau-mouche pèse 2 g et qu'une baleine bleue pèse 1.38 x 10 puissance
5 kg ,
combien
faudrait-il d'oiseaux-mouches pour que leur masse totale soit égale à celle
d'une baleine bleue ?
Donner
le résultat en notation scientifique .
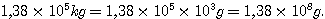
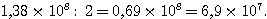
ACTIVITES GEOMETRIQUES ( 12 points )
Exercice n°1 :
La hauteur d’une pyramide mesure 8,5 cm. Sa base est un
rectangle de longueur 10 cm et de largeur 6 cm.
Calculer son volume.
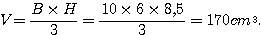
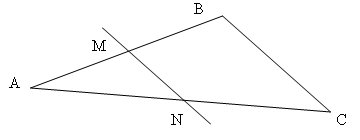
Exercice n°2 : Les dimensions ne sont pas respectées.
Sur la figure suivante, les droite ( MN ) et ( BC ) sont
parallèles.
On donne :
AB = 4,5 cm ; AM = 3,6 cm ; AN = 3,2 cm ; BC = 2 cm.
Calculer AC et MN.
Dans le triangle ABC on sait que M appartient à [AB], que
N appartient à [AC] et que (MN) // (BC).
D'après le théoréme de de Thalès,
on en déduit que:
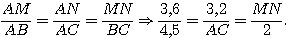
donc AC = 4,5 × 3,2 : 3,6 = 4. et MN = 3,6 × 2 : 4,5 =
1,6 .
Donc AC = 4 cm et MN = 1,6 cm
Exercice n°3 :
Soit C un cercle de diamètre [ BC
] avec BC = 15 cm.
Placer un point A sur le cercle C tel que AB = 12 cm.
1) Faire la figure.
2) Démontrer que le triangle ABC est rectangle.
"Si un
triangle est inscrit dans un demi-cercle de diamètre un de ses côté, alors I
est rectangle"
Donc ABC est rectangle en A.
3) Calculer AC.
Dans le triangle ABC, rectangle en A, d'après le théorème de Pythagore:
AB² + AC² = BC² ; donc AC² = BC² - AB² = 15² - 12² = 225 - 144 = 81 .
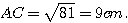
4) Calculer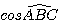 
et en déduire la
mesure de l’angle 
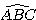( valeur arrondie au
degré près ).
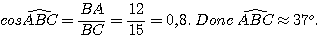
5) Calculer l’aire du triangle ABC.
A = L × l : 2 = 12 × 9 : 2 = 54 cm² .
PROBLEME ( 12 points )
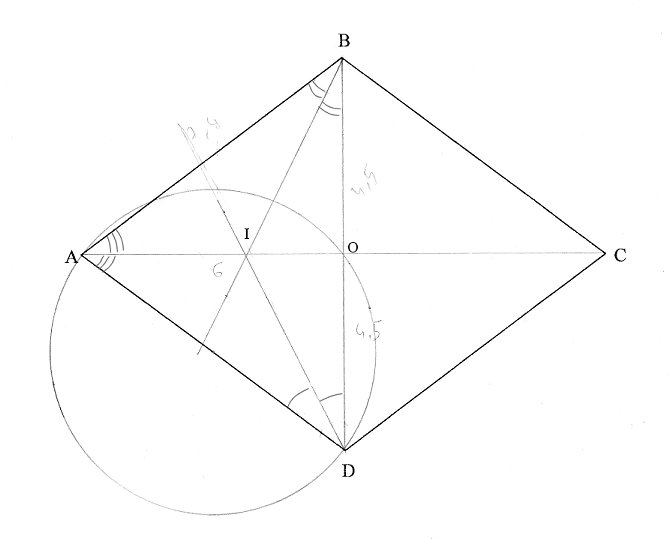
Soit ABCD un losange de centre O
tel que AO = 6cm ;OD = 4,5cm;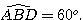 
.
1) Compléter la figure ci - dessous au fur et à mesure.
2) a) Quelle est la nature du triangle ABD ?
Quelle propriété du losange permet de
justifier la réponse ?
Tous les côtés d'un losange sont égaux, donc ABD est un triangle isocèle en A .
b) Quelle est la nature du
triangle AOB ?
Quelle propriété du losange permet de
justifier la réponse ?
"Les diagonales d'un losange
sont perpendiculaires"
Donc AOB est rectangle en O
.
c) Tracer le cercle circonscrit au triangle AOD. Expliquer.
AOD étant rectangle, il est
inscriptible dans un cercle de diamètre son hypoténuse.
Le diamètre du cercle
est donc [AD].
3) Que représente la droite ( AO ) pour le triangle ABD ? Justifier la ( ou les ) réponse ( s ).
ABD étant isocèle en A, (AO) est à la fois médiane, hauteur, médiatrice et bissectrice.
4) Calculer AB.
Dans AOB rectangle en O, d'après le théorème de Pythagore:
AB² =
AO² + BO² = 6² + 4,5² = 36 + 20,25 = 56,25
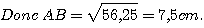
5) Calculer l’aire du losange ABCD.
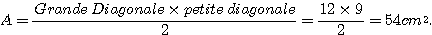
6) Donner la valeur arrondie à l’unité de l’angle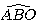 
.
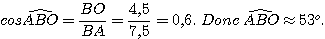
7) Construire la bissectrice de l’angle 
. Elle coupe la droite ( AO ) en I.
Voir
figure.
8) Citer les trois bissectrices des angles du triangle ABD.
Les trois bissectrices de ABD sont (AO); (DI) et (BI) .
9) Que représente le point I pour le triangle ABD?
I représente le centre du cercle inscrit au triangle ABD.
