CORRECTION DEVOIR COMMUN N°1 de 4ème  

                 Décembre  2007

Activités numériques (18 points)

Exercice 1 :

A = (+8) + (-7,3) + (-5) + (+9)– (-7,3) - (+5) = 8 - 7,3 - 5 + 9 + 7,3 - 5 = 17 - 10 = 7

B = 23 – 12 × 3 + 8 = 23 - 36 + 8 = 31 - 36 = - 5

C = 15 + 3 × ( 4 – 6 ) = 15 + 3 × (-2) = 15 - 6 = 9

Exercice 2 :  

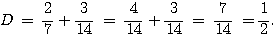
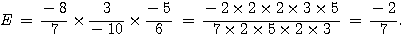
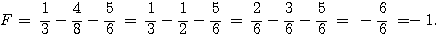
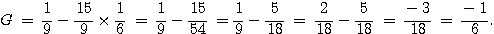
Exercice 3 :

a) Pour calculer 7% de 70g , on fait:

7 × 70 : 100 = 490 : 100 = 4,9.  La barre énergétique contient 4,9g de matières grasses.     

b)      Tableau de proportionnalité:

            Pour trouver le pourcentage on fait un "produit en croix", d'où la réponse: 163 × 100 : 250 = 65,2.

            Donc le sandwich contient 65,2% de matières grasses!

Exercice 4 :

a)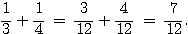       

Il a dépensé les 7/12 de son argent de poche.

b)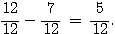     

Il lui reste les 5/12 de son argent de poche

c)      On peut faire le tableau:

    On trouve:  12 × 30 : 5 = 72.  Il avait au départ 72 €.

Exercice5 :

a)      Compléter le tableau suivant :

b)      1h30min = 60 + 30 = 90min  ce qui correspond à 6 + 12 = 18 .

    Il paie 18 € pour 1h30min de communication.

c)      Graphique:

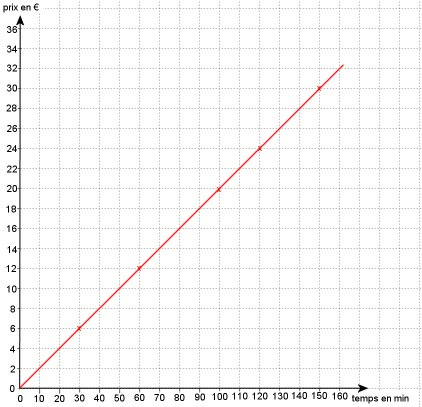
d)      Le graphique exprime une situation de proportionnalité, car c'est une droite passant par l'origine.

Activités géométriques (18 points)

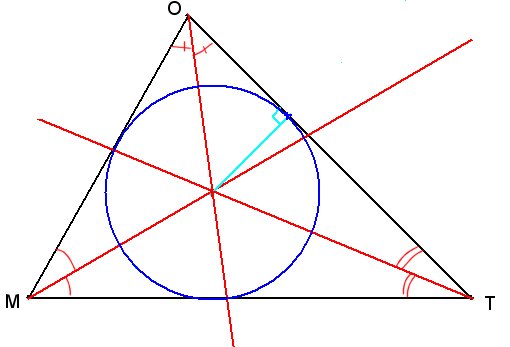
 Exercice 1 :  Construction du cercle inscrit dans le triangle TOM

Exercice 2 :  Les triangles ABC et ADE sont rectangles. On donne : AB = 14,5cm ; BC = 10,5cm ; AE = 9,6cm et DE = 2,8cm.

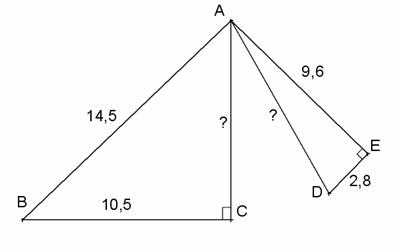
a)      Calcul de AC

Dans le triangle ABC rectangle en C, d'après le théorème de Pythagore:

 AB² = BC² + AC² ; d'où  AC² = AB² - BC² = 14,5² - 10,5² = 210,25 - 110,25 = 100

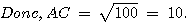
 AC = 10cm

b)      Calcul de AD

De même, dans ADE rectangle en E: AD² = AE² + DE² = 9,6² + 2,8² = 92,16 + 7,84 = 100. Donc AD = 10cm.

c)      Le point A est équidistant de C et de D car AC=AD=10cm; donc il appartient à la médiatrice de [CD] .

Exercice 3 :  Construction.

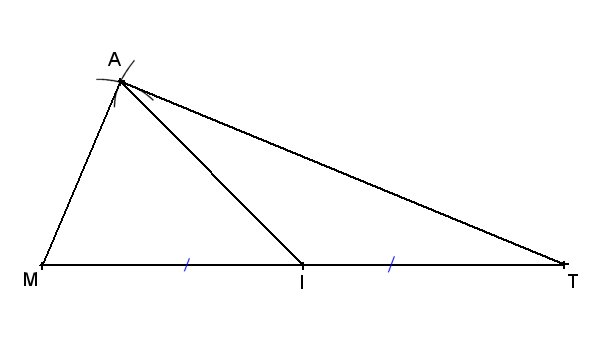
a)      Calculons: MA² + AT² = 12² + 5² = 144 + 25 = 169

                       MT² = 13² = 169

On remarque que MT² = MA² + AT² . D'après le théorème réciproque de Pythagore, le triangle MAT est rectangle en A.

b)      Aire d'un triangle rectangle:

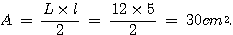
c)      Si I est le milieu de [MT], alors [AI] est la médiane du triangle MAT, issue du sommet de l'angle droit.

Sa longueur est égale à la moitié de l'hypoténuse.

Donc AI = 13:2 = 6,5cm.

Exercice 4 : Construction.

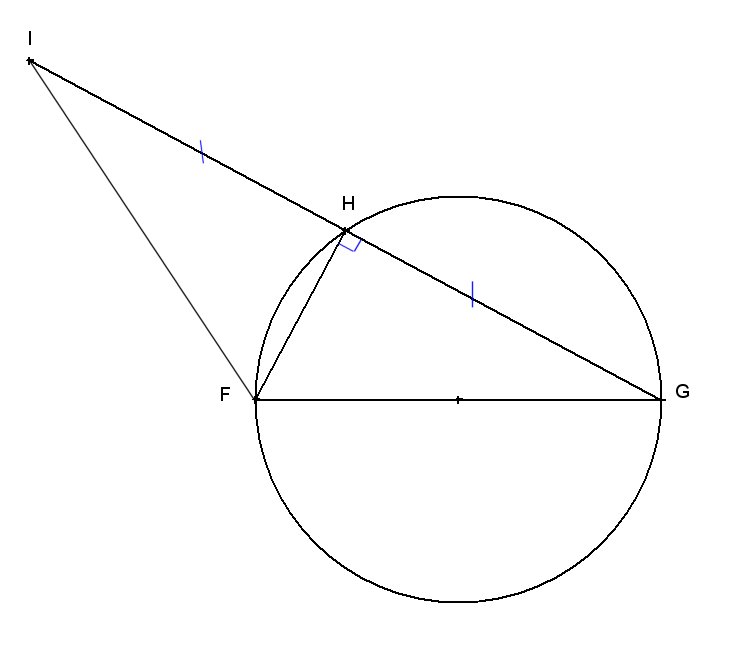
a)      "Si un triangle est inscrit dans un demi-cercle de diamètre un de ses côtés, alors il est rectangle".

Donc FGH est rectangle en H.

b)      Dans FGH rectangle en H, d'après le théorème de Pythagore:

       GH² = FG² - FH² = 10,2² - 4,8² = 104,04 - 23,04 = 81

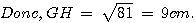
c)      Comme I est le symétrique de G par rapport à H, alors H est le milieu de [GI].

De plus, (FH) est perpendiculaire à (GI). Donc (FH) est la médiatrice de [GI].

F est sur la médiatrice de [GI]; il est donc équidistant de G et de I.

Donc le triangle FGI est isocèle de sommet principal F.

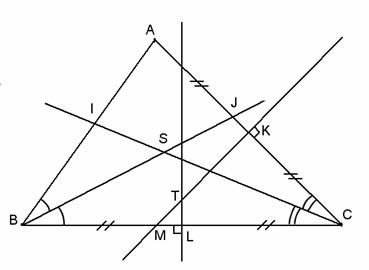
Exercice 5 :