
Devoir Commun de Mathématiques de 4ème / janvier 2005
Exercice n°1 : Calculer : A = 12 - 3 × (- 4) + 7 × (2 -3 - 11 ) -12 × 5
Exercice n°2 : Calculer B et C , donner les résultats sous forme de fractions simplifiées :
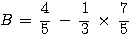

Exercice n°3 : Calculer :
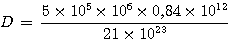
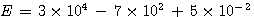
Exercice n°4 : Mettre en notation scientifique :
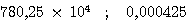
Exercice n°5 :
On donne les résultats obtenus par 25 élèves de quatrième au dernier contrôle de mathématiques ( note sur 20 ).
Notes : 7 ; 13 ; 16 ; 3 ; 10 ; 10 ; 19 ; 18 ; 5 ; 7 ; 13 ; 7 ; 16 ; 18 ; 13 ; 5 ; 10 ; 7 ; 18 ; 5 ; 5 ; 7 ; 18 ; 13 ; 7.
1) Calculer la moyenne de la classe.
2) Compléter le tableau n°1 :
|
N: Note |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Effectif |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fréquence % |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) a) Compléter le tableau n°2 :
|
N: Note |
|
|
|
|
|
|
Effectif |
|
|
|
|
|
|
Eff cum |
|
|
|
|
|
b) Calculer, à partir de ce tableau, la moyenne de la classe.
c) Tracer l’histogramme des effectifs .
Exercice n°1 :
On considère le quadrilatère EFGH ci-contre. I est le milieu de [FG], J est le milieu de [EG]. 1) Démontrer que les droites (IJ) et (EF) sont parallèles. 2) La droite (d) parallèle à (EH) passant par J coupe [GH] en K. Démontrer que K est le milieu de [GH]. 3) Démontrer que la droite (IK) est parallèle à la droite (FH). |
|
Exercice n°2 :
|
La figure ci-contre n’est pas en vraie grandeur 1) Dessiner en vraie grandeur la figure ci-contre. 2) Calculer BD. 3) En déduire que BCD est un triangle isocèle. |
|
Exercice n°3 :
1) Construire le triangle IJK tel que IJ = 5,1 cm , JK = 2,4 cm et IK = 4,5 cm.
2) Le triangle IJK est - il rectangle ?
Justifier votre réponse.
Exercice n°4 :
| Paul
veut installer chez lui un bac à fleurs. Il doit le fixer à 6,5 m du sol.
L'échelle dont il se sert mesure 7 m de long.
A
quelle distance du pied du mur doit-il placer l’échelle pour que son sommet
soit juste au niveau du bac à fleurs ?
( Donner une valeur approchée au dixième ) |
|
La figure est à compléter au fur et à mesure du problème sur la feuille annexe.
On considère un cercle z de centre O et de diamètre [AD] tel que AD = 10 cm.
B est un point du cercle z tel que AB = 5 cm.
1) Démontrer que le triangle ABD est rectangle en B.
2) Calculer BD puis donner une valeur arrondie à 0,1 près.
3) Démontrer que le triangle OAB est équilatéral.
4) Soit E le symétrique de A par rapport à B.
Démontrer que (BO) est parallèle à (ED).
Calculer ED.
5) La perpendiculaire en A à la droite (AB) coupe le cercle z en F.
Démontrer que ABDF est un rectangle.
6) Tracer la médiatrice D de [AF].
Montrer que O appartient à la droite D.