Correction devoir Commun de Mathématiques de 4ème
ALGEBRE (18 points)
Exercice 1:
Calculer en détaillant:
A = (-3) × ( -2 + 7 ) + 3 × (-5) = (-3) × 5 + 3 × (-5) = -30
Exercice 2:
Calculer et
donner le résultat sous forme de fraction simplifiée:
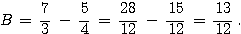
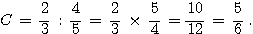
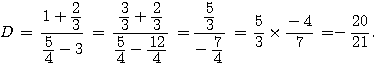
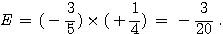
Exercice 3:
a) Simplifier (réduire) l'expression suivante: F = 3a – 5b + b + 7a = 10a - 4b
b) Calculer 10a – 4b pour a = 2 et b = 5: 10a - 4b = 10 × 2 - 4 × 5 = 20 - 20 = 0
Exercice 4:
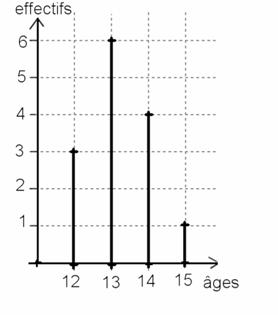
|
âges |
12 |
13 |
14 |
15 |
|
Effectif
|
3 |
6 |
4 |
1 |
|
Effectif cumulé croissant |
3 |
9 |
13 |
14 |
|
Fréquence en % |
21,4 |
42,9 |
28,6 |
7,1 |
|
Angle |
38,5 |
77,2 |
51,5 |
12,8 |
Diagramme semi-circulaire :
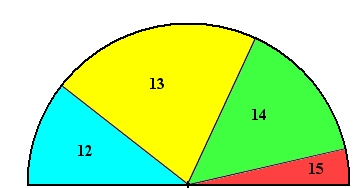
Exercice 5:
Voici,
regroupées par classe, les notes obtenues au devoir d'Espagnol des élèves de 4ème
C.
|
Note N |
0 ≤ N < 5 |
5 ≤ N < 10 |
10 ≤ N <
15 |
15 ≤ N <
20 |
|
Effectifs |
2 |
5 |
12 |
6 |
a)Combien d'élèves y a-t-il en 4ème C? 2+5+12+6 = 25 élèves.
b) Combien d'élèves n'ont pas la moyenne? 7 élèves n'ont pas la moyenne.
c) Calculer la moyenne de cette classe à ce devoir.
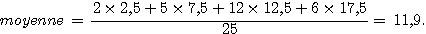
d) Construire l'histogramme représentant le nombre d'élèves en fonction de leur note.

GEOMETRIE (18 points)
Exercice 1:
On considère un triangle ABC tel que : BC = 10,4 cm ; AB = 9,6 cm ; AC = 4 cm.
1) Faire une figure au verso de la feuille annexe
2) Démontrer que le triangle ABC est rectangle.
3) Soit O le centre du cercle circonscrit au triangle ABC.
a) Préciser, en justifiant, la position du point O.
b) Placer le point O et tracer le cercle circonscrit au triangle ABC.
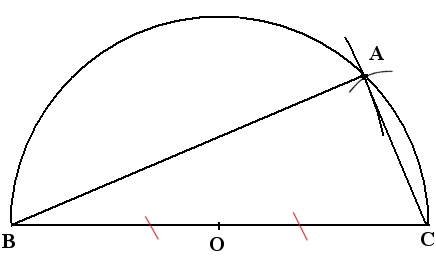
2) Calculons: AB² = 9,6² = 92,16; AC² = 4² = 16 ; BC² = 10,4² = 108,16.
AB² + AC² = 92,16 + 16 = 108,16
On remarque que AB² + AC² = BC².
D'après le théorème réciproque de Pythagore, ABC est rectangle en A
3) Un triangle rectangle est inscriptible dans un cercle de diamètre son hypoténuse.
Le centre O du cercle est donc le milieu de [BC].
Exercice 2:
On considère un cercle C de centre O et de rayon 5 cm. On appelle [RS] un diamètre de C et E un point de C tel que ES = 8 cm..
1) Faire une figure au verso de la feuille annexe.
2) a) Quelle est la nature du triangle RES ? Justifier.
b) Montrer que [RE] mesure 6cm.
3) a) Tracer la droite (d) tangente en R au cercle C. La droite (d) coupe la droite (SE) en K.
b) Sachant que [KR] mesure 7,5 cm calculer la longueur KS
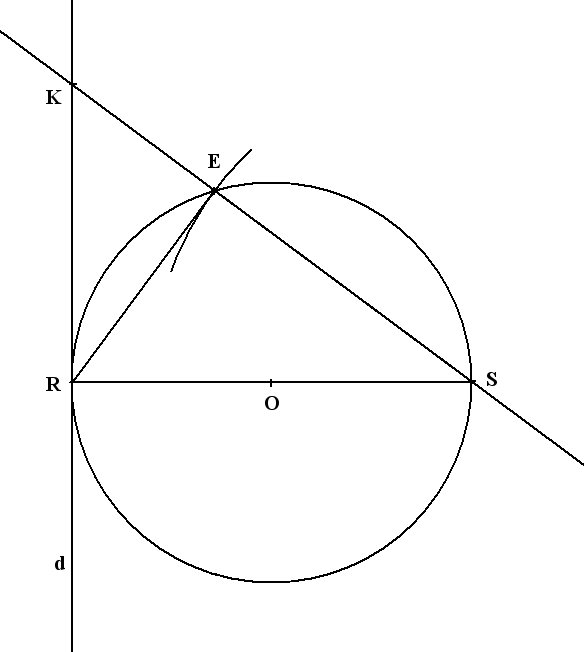
2) a) RES est inscrit dans un demi cercle de diamètre son côté [RS]
" Si un triangle est inscrit dans un demi cercle de diamètre un de ses côtés, alors il est rectangle"
Donc RES est rectangle en E.
b) Dans RES rectangle en E, d'après le théorème de Pythagore:
RE² = RS² - ES² = 10² - 8² = 100 - 64 = 36.
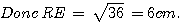
3) La droite d étant tangente en R à (RS), d est perpendiculaire à (RS)
Le triangle KRS est donc rectangle en R
D'après le théorème de Pythagore:
KS² = KR² + RS² = 7,5² + 10² = 56,25 + 100 = 156,25.
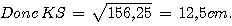
Exercice 3: (Répondre dans
l'ordre aux questions en justifiant les réponses)
On considère le triangle MAT rectangle en A tel que MT =
7,3cm.
Le point I est le milieu de [AM]; le point J est le milieu
de [AT].
a) Que peut-on dire des droites (IJ) et (MT)?
b) Calculer IJ
c) Sachant que AT = 5,5cm, calculer AM
d) Calculer l'aire du triangle AIJ
e) Calculer l'aire du triangle MAT
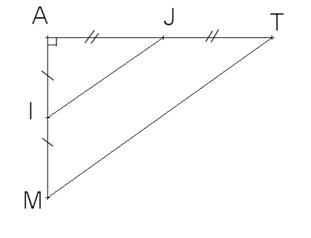
a) I est le milieu de [AM] et J est le milieu de [AT]
" La droite qui joint les milieux de deux côtés d'un triangle est parallèle au troisième côté".
Donc (IJ) est parallèle à (MT).
b) "La longueur du segment qui joint les milieux de deux côtés d'un triangle est égal à la moitié du troisième côté"
Donc IJ = MT / 2 = 7,3 : 2 = 3,65cm.
c) MAT étant rectangle en A, d'après le théorème de Pythagore:
AM² = MT² - AT² = 7,3² - 5,5² = 53,29 - 30,25 = 23,04
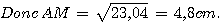
d) Comme I est le milieu de [AM], on a AI = AM/2 = 4,8 : 2 = 2,4cm
De même, AJ = AT : 2 = 5,5 : 2 = 2,75cm
Comme AIJ est rectangle en A,
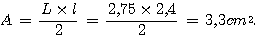
e) MAT est rectangle en A.
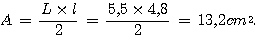
(On remarque que si les longueurs du triangle MAT sont le double de celles de AIJ, l'aire de MAT est 4 fois égale à celle de AIJ)