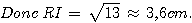
DEVOIR COMMUN DE MATHEMATIQUES DE 4°

CORRECTION

 

 


Activités géométriques (18 points) 

Exercice 1:

1°) Comme I est le milieu de [TI], on a TI = 2 × TA = 2 × 3 = 6cm

Dans le triangle TRI, rectangle en I, d'après le théorème de Pythagore:

RI² = TR² - TI²

     = 7² - 6²

     = 49 - 36 = 13

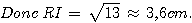
2°) Dans TAN, rectangle en A:

cos T = TA / TN

D'où TN = 3 : cos 58 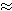 5,7cm

Exercice 2 : 

Dans le triangle ABC, le point M est sur [AB) et le point P est sur [AC] tels que (MP) est parallèle à (BC).

D'après le théorème de Thalès:

 

 

 

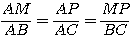
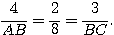
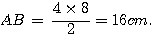
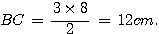
Périmètre: P= 16 + 12 + 8 = 36 cm.

 

Exercice 3 :

Volume d’une pyramide :

 

 

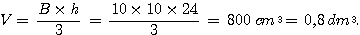
Exercice 4 :

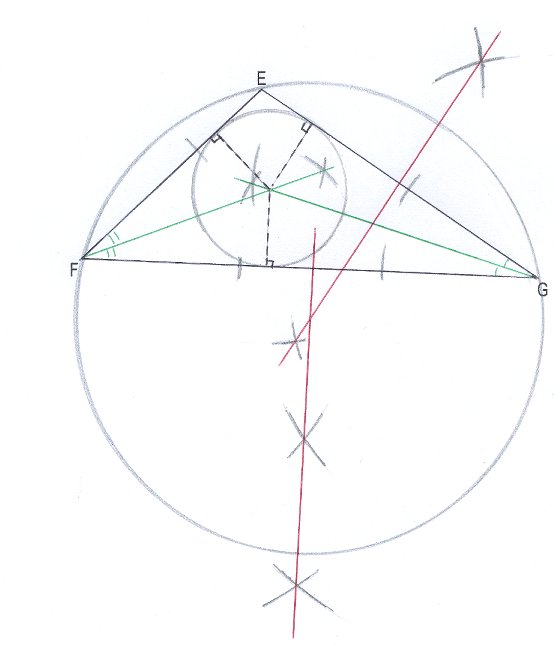
1°) figure: voir ci-contre

2°) Calculons:

MA² = 7,3² = 53,29

MS² + AS² = 4,8² + 5,5² = 23,04 + 30,25 = 53,29

Donc MA² = MS² + AS²

D'après le théorème réciproque de Pythagore,
MAS est rectangle en S.

3°) Dans le triangle rectangle MAS:

4°) H et T étant les symétriques respectifs de A et M par rapport à S, les diagonales [MT] et [HA] ont le même milieu S.

Donc MATH est un parallélogramme.

De plus, ces diagonales sont perpendiculaires.

Le quadrilatère MATH est donc un losange.

 

5 :

 

 

 

 

Activités numériques (18 points) 

Exercice 1 :

 

A =  a – 2b – 3ab  +  4  = 4 - 2× (-3) - 3 × 4 × (-3) + 4 = 4 + 6 + 36 + 4 = 50

 

Exercice 2 :

 

 

 

 

Exercice 3 :

 

E = 2(-x + 3) +3(2x – 5) = -2x + 6 + 6x - 15 = 4x -9

F = (2x – 1)(3x – 5) = 6x² - 10x - 3x + 5 = 6x² -13x + 5

 

Exercice 4 :

 

1. x représente le nombre de CD.

2.            4 × 6 + x × 9 = 96

               24 + 9x = 96

                      9x = 96 - 24

                      9x = 72

                        x = 72 : 9 = 8

3. Réponse: il peut acheter huit CD.

 

Exercice 5 :

 

12x - 3 = 11 + 5x

12x - 5x = 11 + 3

7x  = 14

x = 14 : 7 = 2

Réponse: x = 2

Exercice 6 :

1. Périmètre d'un rectangle: P = ( L + l ) × 2 = ( 2x + 5 + x + 1 ) × 2 = ( 3x + 6 ) × 2 = 6x +12

2. Si P = 54 , alors:

      6x + 12 = 54

              6x = 54 - 12

              6x = 42

                x = 42 : 6 = 7

 Réponse: x = 7

 

Exercice 7 :

Utilisons un tableau de proportionnalité:

Distance en km

1,5

d

Temps passé en minutes

3

10

 

3 × d = 1,5 × 10

donc 3 × d = 15; d'où d = 15 : 3 = 5

La distance parcourue en 10 min est de 5 km.