MATHEMATIQUES

DEVOIR COMMUN N°2 de 4ème

 

Mai  2008

L’usage de la calculatrice est autorisé, mais le prêt est interdit.

La présentation, la rédaction et l’orthographe interviendront pour un total de 4 points.

 


Activités numériques (18 points)

Exercice 1 :  Calculer en détaillant les étapes intermédiaires ; donner le résultat sous forme de fraction simplifiée.

              

Exercice 2 :  a ) Développer et réduire :   C = 2 ( 3x – 4 ) + 5 ( x + 1 )

                      b) Calculer C pour x = 0 .

 

Exercice 3 :  a ) Développer et réduire :   D = ( 4x – 7 )  ( x + 2 )

                      b) Calculer D pour x = -2

 

Exercice 4 : Calculer E et donner le résultat sous la forme d’une puissance de 10 ;
                    calculer F et donner le résultat sous la forme d’un nombre entier.  

 

              

 

Exercice 5 : Donner l’écriture scientifique des nombres suivants :  

a)      La distance de la terre au soleil est estimée à 149 597 870,691 km

b)      Le diamètre d’un noyau atomique peut aller
jusqu’à 0,000 000 000 015 mm

c)      Actuellement, le film « Bienvenue chez les ch’tis » a fait plus
de 22 millions d’entrées

 

 

 

Exercice 6 : Résoudre les équations suivantes :

 

a)      2x + 6 = 7

b)      3x – 12 = 5x + 7

c)         

 

 

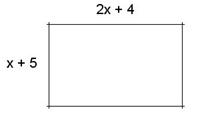
Exercice 7 : Un fermier dispose d’un champ rectangulaire dont les mesures en mètres sont sur le schéma ci-contre.

a)      Calculer le périmètre de ce champ pour x = 2

b)      Quelle équation doit-on résoudre pour que le rectangle soit un carré ? Résoudre cette équation.  

 

 

 

Exercice 8 : Caroline a deux fois l’âge de Zoé moins cinq ans. Zoé a la moitié de l’âge de Pierre.
Si on additionne les âges de Pierre, Caroline et Zoé, on obtient 25 ans. Soit x l’âge de Zoé.

a)      Exprimer en fonction de x l’âge de Caroline.

b)      Exprimer en fonction de x l’âge de Pierre.

c)      Traduire la situation par une équation puis la résoudre.

d)      Quel est l’âge de chaque enfant ?

 

 

Activités géométriques (18 points)

Attention : toutes les figures ne sont pas représentées en dimensions réelles

 

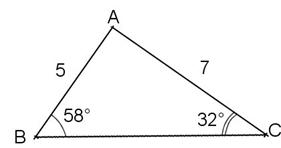
 Exercice 1 :  En observant la figure ci-contre :

a)      Démontrer que ABC est un triangle rectangle

b)      Calculer BC (valeur exacte puis
arrondie à 10-1 près)

c)      Calculer l’aire de ABC

 

 

 

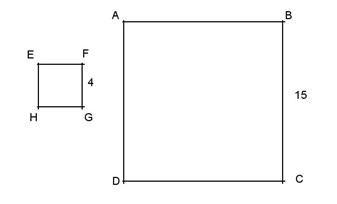
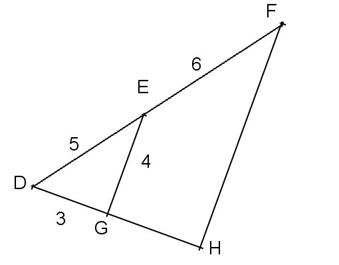
 Exercice 2 :  Pour la figure suivante, on sait que (EG) est parallèle à (FH) et que DG = 3cm ;
 DE = 5cm ; GE = 4cm ; EF = 6cm.:

 

a)      Calculer DH et FH

b)      Calculer le périmètre du trapèze EFHG

c)      Démontrer que DEG est un triangle rectangle

d)      En déduire que le triangle DFH est un triangle rectangle.

 

 

 

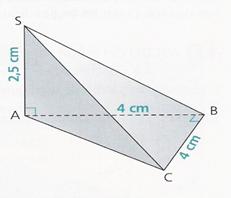
Exercice 3:    

SABC est une pyramide dont la base ABC est
un triangle rectangle et isocèle en B.
L’arête [SA] est perpendiculaire à la base ABC, elle est donc perpendiculaire à (AB) et à (AC), c’est la hauteur de la pyramide.

a)      Sans effectuer de calcul, construire sur la copie le patron de la pyramide SABC.

Calculer la longueur SB, arrondie au mm. Vérifier sur le patron.

 

 

 

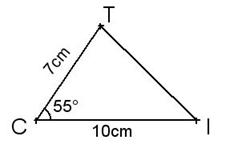
Exercice 4 :

 

a)      Construire la réduction du triangle CIT de coefficient 0,8 (en tenant compte des mesures indiquées).

b)      ABCD est un agrandissement du carré EFGH. Calculer le coefficient d’agrandissement.