BREVET BLANC
Décembre 2003
L’usage de la
calculatrice est autorisé, mais le prêt est interdit.
La
présentation, la rédaction et l’orthographe interviendront pour un total de 4
points.
Activités
numériques (12 points)
Exercice 1 :
On considère les nombres :
1) Calculer et donner A sous forme d’une fraction irréductible.
2) Ecrire B sous la forme a où a est un entier.
3) Calculer et donner C sous forme d’une fraction irréductible.
Exercice 2 :
On considère l’expression : D = (4x – 1)2 – (x + 3) (4x – 1).
1) Développer puis réduire D
2) Calculer D pour x = -2
Exercice 3 :
1) Calculer le plus grand diviseur commun de 540 et 300
2) Une pièce rectangulaire de 5,40m de long et de 3m de large est recouverte, sans découpe, par des dalles de moquette carrées, toutes identiques.
a) Quelle est la mesure du côté de chacune de ces dalles, sachant que l’on veut le moins de dalles possibles ?
b) Calculer alors le nombre de dalles utilisées.
Exercice 4 :
Voici les notes obtenues par 25 élèves d’une classe de troisième au dernier Brevet blanc :
3 ; 3 ; 5 ; 5 ; 5 ; 5 ; 7 ; 7 ; 7 ; 7 ; 7 ; 9 ; 10 ; 10 ; 11 ; 11 ; 12 ; 13 ; 13 ; 13 ; 14 ; 15 ; 15 ; 16 ; 18 .
a) Calculer la moyenne des notes obtenues
b) Déterminer la médiane
c) Calculer l’étendue
d) Compléter le tableau et faire l’histogramme des effectifs.
|
Note n |
0 £ n < 4 |
4 £ n < 8 |
8 £ n < 12 |
12 £ n < 16 |
16 £ n £ 20 |
|
Effectif |
|
|
|
|
|
e) Calculer la moyenne des notes à partir du regroupement par classes du tableau.
Activités
géométriques (12 points)
|
|
Exercice 1 :
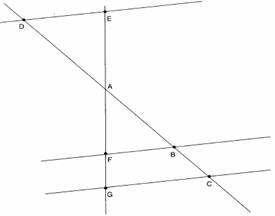
Sur la figure ci-contre, qui n’est pas dessinée en vraie grandeurs, les droites (BF) et (CG) sont parallèles.
1. On donne: AB = 5 ; BC = 4 et AF = 3
Calculer AG puis FG
2. On donne: AD = 7 et AE = 4,2
Démontrer que les droites (ED) et (BF) sont parallèles.
Exercice 2 :
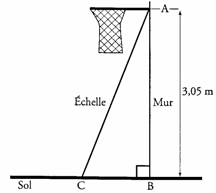
1. Paul veut installer chez lui un panier de basket. Il doit le fixer à 3,05 m du sol. L’échelle dont il se sert mesure 3,20 m de long.
À quelle distance du pied du mur doit-il placer l'échelle pour que son sommet soit juste au niveau du panier ? (Donner une valeur approchée au cm près.)
2. Calculer l'angle formé par l'échelle et le sol. (Donner une valeur approchée au degré près.)
|
|
Exercice 3 :
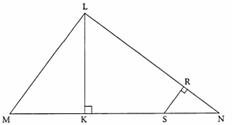
On considère la figure ci-contre.
On donne MN = 8 cm; ML = 4,8 cm et LN = 6,4
cm.
On ne demande pas de refaire la figure.
l. Démontrer que le triangle LMN est rectangle.
2. Calculer la valeur arrondie au degré de la mesure de l'angle Æ
3. Soit K le pied de la hauteur issue de L.
a.
Calculer l’aire du triangle LMN
b. en déduire que LK = 3,84 cm.
4. Soit S le point de [MN] tel que NS = 2 cm, la perpendiculaire à la droite (LN) passant par S coupe le segment [LN] en R. Calculer RS.
Problème
(12 points)
Soit un triangle ADB rectangle en D, tel que DA = 12cm et DB = 16cm.
1. a) Construire le triangle ADB.
b) Calculer AB.
2. a) Placer le point C du segment [BA] tel que BC = 8.
Tracer le cercle C
de diamètre[BC].
Le cercle C
recoupe la droite (BD) en E.
b) Démontrer que le triangle BEC est rectangle en E.
c) En déduire que les droites (AD) et (CE) sont parallèles.
d) Calculer EC et BE.
3. On note M le milieu de [AB], et H le point d’intersection des droites
(EC) et (DM).
Calculer MC, puis CH.
4. a) Prouver que les angles Æ et Æ ont même mesure
b) Déterminer au degré près les angles Æ ; Æ et Æ