BREVET BLANC
Décembre 2002
L’usage de la
calculatrice est autorisé, mais le prêt est interdit.
La
présentation, la rédaction et l’orthographe interviendront pour un total de 4
points.
Activités
numériques (12 points)
Exercice 1 :
On considère les nombres :
A = ![]() B =
B = ![]() C =
C = ![]()
1) Calculer A et simplifier au maximum le résultat.
2) Donner l’écriture scientifique de B
3) Ecrire C sous la forme a où a est un entier.
Exercice 2 :
F = (x - 3)(2x - 5) + (x - 3)²
1) Réduire F après avoir développé les produits.
2) Factoriser F.
Exercice 3 :
Les températures moyennes enregistrées à Paris du 3 au 12 novembre 1999 sont exprimées en degré Celsius :
|
Date |
Température |
|
Date |
Température |
|
3 novembre |
13° |
|
8 novembre |
12° |
|
4 novembre |
11° |
|
9 novembre |
12° |
|
5 novembre |
12° |
|
10 novembre |
9° |
|
6 novembre |
11° |
|
11 novembre |
8° |
|
7 novembre |
10° |
|
12 novembre |
9° |
1) Quelle est l’étendue de cette série ?
2) Quelle est sa médiane ?
3) Quelle est sa moyenne ?
Exercice 4 :
Le tableau ci-dessous donne, selon le prix, les effectifs des sèche-linge vendus dans une grande surface sur une année.
|
Prix unitaire p en € |
effectif |
Effectif cumulé |
|
|
10 |
|
|
|
28 |
|
|
|
2 |
|
1) Recopier ce tableau en complétant la colonne des effectifs cumulés
2) Quel est le pourcentage de sèche-linge vendus moins de 550€ pièce ?
3) Quel est, sur cette série, le prix moyen d’un sèche-linge ?
Activités
géométriques (12 points)
 Exercice
1 :
Exercice
1 :
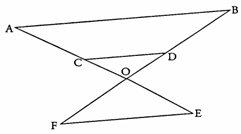
Sur la figure ci-contre, les droites (AB) et (CD) sont parallèles.
OA = 8 ; OB = 10 ; OC = 2 ; OE = 6,4 ; OF = 8
(les dimensions ne sont pas respectées sur la
figure)
1) Calculer la longueur OD.
2) Démontrer que les droites (AB) et (EF) sont parallèles.
Exercice 2 :
Soit DEF un triangle tel que DE = 9.6 cm , EF = 10.4 cm et DF = 4 cm .
(Il n’est pas demandé de faire une figure)
1) Démontrer que le triangle DEF est rectangle .
2) Calculer sin Æ et en déduire la valeur arrondie à 1 degré près de l’angle Æ
Exercice 3 :
Tracer C un cercle de diamètre [BC] tel que BC = 6 cm
1) Placer un point A sur le cercle C tel que Æ = 45 °
2) Démontrer que le triangle ABC est un triangle rectangle isocèle.
3) Sachant que cos 45° = ; sin 45° = et tan 45° = 1
a) calculer la valeur exacte du segment [AB]
b) calculer la valeur exacte de l’aire du triangle ABC
Exercice 4 :
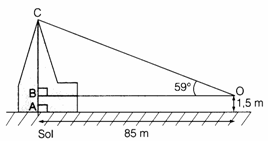
On veut mesurer la hauteur d'une cathédrale. Grâce à un instrument de mesure placé en O, à 1,5 m du sol et à 85 m de la cathédrale, on mesure l'angle Æ et on trouve 59°.
On admettra que: AB = 1,5m.
1) Déterminer la longueur CB au dixième de mètre le plus proche.
2) En déduire la hauteur de la cathédrale.
Problème
(12 points)
Le dessin est à faire
sur la copie.
Tracer un segment [BC] de longueur 6 cm et construire sa médiatrice D.
D coupe [BC] en H. Soit A un point de D tel que HA = 4 cm.
1) Quelle est la nature du triangle ABC? Justifier la réponse.
2) Montrer que AB = 5 cm.
3) Soit E le point de [BC] tel que BE = 2 cm. La droite d passant par E et parallèle à D coupe [AB] en F.
a) Montrer que ![]()
b) En déduire la valeur exacte de BF.
4) Soit I le centre du cercle circonscrit au triangle ABH.
Soit J le centre du cercle circonscrit au triangle ACH.
a) Quelle est la position du point I ? Justifier.
b) Démontrer que les droites (IJ) et (BC) sont parallèles.
c) Calculer IJ.
5) Quelle est la nature du quadrilatère AIHJ? Justifier la réponse.