I  ACTIVITES NUMERIQUES

Exercice 1

1. Calculons A :

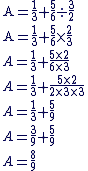
2. Calculons B :

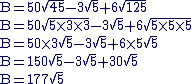
3. Calculons C :

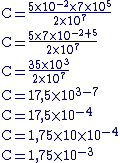
Exercice 2

1. Développons et réduisons D :

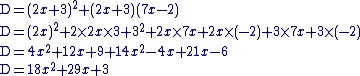
2. Factorisons D :

3. Calculons D pour = -4 :
Pour = -4 :
D = 18 × (-4)² + 29 × (-4) + 3
D = 18 × 16 - 29 × 4 + 3
D = 288 - 116 + 3
D = 175

4. Résolvons l'équation :

Un produit de facteurs est nul si l'un au moins des facteurs est nul, et réciproquement.
ou
ou
ou
Les solutions de l'équation sont et

Exercice 3

1. Nombre maximal de personnes pouvant bénéficier de ces friandises :
Chacun doit avoir le même nombre de sucettes et le même nombre de bonbons, le nombre n de personnes divise donc le nombre de sucettes et le nombre de bonbons. Le nombre n est donc un diviseur de 84 et 147.
De plus, on veut que le nombre n de personnes bénéficiant des friandises soit maximal, donc n est le plus grand diviseur commun de 84 et 147 (le PGCD de 84 et 147).
Déterminons le PGCD de 84 et 147 :
>> Par la méthode des soustractions successives :
PGCD(147 ; 84) = PGCD(84 ; 63) car 147 - 84 = 63
PGCD(84 ; 63) = PGCD(63 ; 21) car 84 - 63 = 21
PGCD(63 ; 21) = PGCD(42 ; 21) car 63 - 21 = 42
PGCD(42 ; 21) = PGCD(21 ; 21) car 42 - 21 = 21
PGCD(21 ; 21) = 21
D'où : PGCD(147 ; 84) = 21

>> En utilisant l'algorithme d'Euclide :
147 = 84 × 1 + 63
84 = 63 × 1 + 21
63 = 21 × 3 + 0
Le dernier reste non nul est 21, donc PGCD(147 ; 84) = 21
D'où : 21 personnes pourront bénéficier des friandises.

2. Elles auront 84 : 21 = 4 sucettes et 147 : 21 = 7 bonbons chacune.

Exercice 4

1. Résolvons le système :

On multiplie la première équation par (-3) :

On additionne membre à membre :


En remplaçant par 4 dans la première équation, on obtient :
8 × 4 + 3y = 39,5
32 + 3y = 39,5
3y = 39,5 - 32
3y = 7,5
y =
y = 2,5
Le couple (4 ; 2,5) est solution du système.

2. Déterminons le prix d'un ticket pour un adulte et celui d'un ticket pour un enfant :
Soit le prix d'un ticket pour un adulte
Soit y le prix d'un ticket pour un enfant.
" Le premier groupe, composé de 8 adultes et de 3 enfants, paie 39,50 € " se traduit par : 8 + 3y = 39,5
" Le second groupe, composé de 7 adultes et de 9 enfants, paie 50,50 € " se traduit par : 7 + 9y = 50,5
On obtient alors le système suivant :
Nous l'avons résolu à la question précédente.
D'où : le prix d'un ticket pour adulte est de 4 € et celui d'un ticket pour enfant est de 2,5 €.

II GEOMETRIE

Exercice 1

1. Plaçons les points A, B et C :

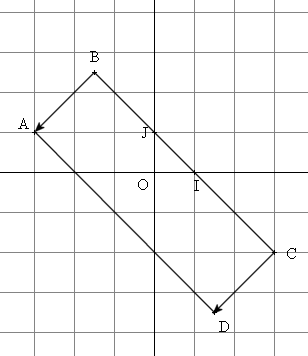
2. Montrons que AC = :

AC² = (3 - (-3))² + (-2 - 1)²
AC² = 6² + (-3)²
AC² = 36 + 9
AC² = 45
D'où : AC = .

3. Démontrons que ABC est un triangle rectangle :
On a d'une part : AB² + BC² = = 4,5 + 40,5 = 45,
et d'autre part : AC² = = 45.
Comme AB² + BC² = AC², alors d'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.

4. Plaçons le point D image de C par la translation de vecteur :
cf graphique

5. Déterminons la nature du quadrilatère ABCD :
On sait que le point D est l'image de C par la translation de vecteur , donc . ABCD est donc un parallélogramme.
De plus, comme ABC est rectangle en B, alors ABCD a un angle droit.
On en conclut que ABCD est un rectangle.

Exercice 2

1.

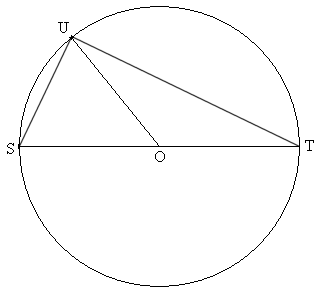
2. Démontrons que STU est un triangle rectangle en U :
On sait que U est un point du cercle de diamètre [ST], donc le triangle STU est rectangle en U.

3. Donnons la valeur arrondie au dixième de l'angle :
Dans le triangle STU rectangle en U, on a :

Donc : °.

4. Déduisons-en une valeur approchée au dixième de :
L'angle au centre et l'angle inscrit interceptent le même arc, donc :

D'où : °.

Exercice 3

1. Montrons que OB = 9 cm :
Dans le triangle OAB rectangle en O, on a :
,
donc OB = OA ×
Donc : OB = 9 cm

2. Montrons que les droites (CD) et (AB) sont parallèles :
On sait que les points A, O, D d'une part et B, O, D d'autre part sont alignés dans le même ordre.
On a :
Donc , d'après la réciproque du théorème de Thalès, on en déduit que les droites (CD) et (AB) sont parallèles.

III PROBLEME

Partie A

1. a) Calculons EF :
Les droites (EA) et (FB) sont sécantes en S.
On sait que EFGH est la section de la pyramide SABCD par le plan parallèle à la base, donc les droites (EF) et (AB) sont parallèles.
D'après le théorème de Thalès, on a : .
De , on en déduit que
D'où : EF = 2,25 cm.

1. b) Calculons SB :
Dans le triangle SAB rectangle en A, on applique le théorème de Pythagore :
SB² = SA² + AB², donc :
SB² = 12² + 9²
SB² = 144 + 81
SB² = 225
Donc : SB =
D'où : SB = 15 cm

2. a) Calculons le volume de la pyramide SABCD :

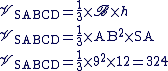
D'où : le volume de la pyramide SABCD est de 324 cm³.

2. b) Le coefficient de réduction permettant de passer de la pyramide SABCD à la pyramide SEFGH est donné par

2. c) Déduisons-en le volume de SEFGH :

D'où : le volume de la pyramide SEFGH est d'environ 5 cm³.

Partie B

1. Montrons que MN = 0,75 :
On sait que MNPQ est la section de la pyramide SABCD par le plan parallèle à la base passant par M, donc les droites (MN) et (AB) sont parallèles.
De plus, les droites (AM) et (BN) sont sécantes en S, alors d'après le théorème de Thalès, on a :
.
De , on en déduit que
D'où : EF = 0,75 (en cm).

2. Montrons que A() = 0,5625 :
L'aire du carré MNPQ en fonction de est donnée par :
A() = MN² =
D'où : A() = 0,5625 (en cm²)

3. Complétons le tableau :

: longueur SM en cm	0	2	4	6	8	10	12
A() : aire du carré MNPQ	0,5625 × 0² = 0	0,5625 × 2² = 2,25	0,5625 × 4² = 9	0,5625 × 6² = 20,25	0,5625 × 8² = 36	0,5625 × 10² = 56,25	0,5625 × 12² = 81

4. Plaçons dans le repère les points d'abscisse et d'ordonnée A() données par le tableau :

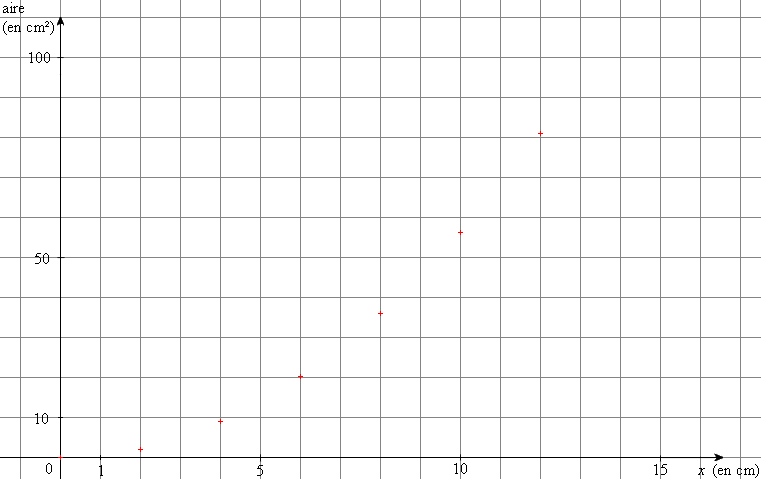
5. Les points d'abscisse et d'ordonnée A() ne sont pas alignés, donc l'aire de MNPQ n'est