Activités numériques (12 points)
 Exercice 1
Exercice 1
Cet exercice est un questionnaire à choix
multiples (QCM). Aucune justification n'est demandée.
Pour chacune des questions, trois réponses sont proposées, une seule est exacte.
Pour chacune des cinq questions, indiquer sur la copie le numéro de la question et recopier la réponse exacte.
1. Quelle est
l'expression développée de 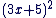 ? ? |
.gif) |
.gif) |
.gif) |
2. Quelle est l'expression qui est
égale à 10 si on choisit la valeur .gif) ? ? |
.gif) |
.gif) |
.gif) |
3. Quelle est la valeur exacte de
.gif) ? ? |
.gif) |
3,464 | .gif) |
4. Quel est le nombre qui est
solution de l'équation .gif) ? ? |
10 | -10 | 2 |
| 5. En 3e A, sur 30
élèves, il y a 40 % de filles. En 3e B, sur 20 élèves, il y a 60 % de filles. Lorsque les deux classes sont réunies, quel est le pourcentage de filles dans le groupe ? |
36 % de filles. | 48 % de filles. | 50 % de filles. |
 Exercice 2
Exercice 2
On donne un programme de calcul : 1. Ecrire les calculs permettant de vérifier si l'on fait fonctionner ce programme avec le nombre —2, on obtient 0.
2. Donner le résultat fourni par le programme lorsque le nombre choisi est 5.
3. a) Faire deux autres essais en
choisissant à chaque fois un nombre entier et écrire le résultat obtenu sous la
forme du carré d'un autre nombre entier (les essais doivent figurer sur la
copie).
b) En est-il
toujours ainsi lorsqu'on choisit un nombre entier au départ de ce programme de
calcul ? Justifier la réponse.
4. On souhaite obtenir 1 comme résultat. Quels nombres peut-on choisir au départ ?
Activités géométriques (12 points)
 Exercice 1
Exercice 1
L'unité de longueur est le centimètre. ABC est un triangle tel que AB = 9 ; AC = 15 ; BC = 12.
1. a) Démontrer que ABC est rectangle en
B.
b) Tracer en vraie
grandeur le triangle ABC sur la copie.
2. E est le point du segment [AB] tel que
AE = 3. F est le point du segment [AC] tel que AF = 5.
a) Placer les points E
et F sur la figure.
b)
Démontrer que la droite (EF) est parallèle à la droite (BC).
3. Calculer l'aire du triangle AEF.
 Exercice 2
Exercice 2
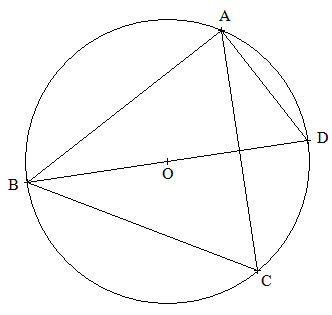
Sur la figure ci-dessus, ![]() ABC est un triangle
équilatéral,
ABC est un triangle
équilatéral, ![]() Le point O est le centre du cercle circonscrit au triangle ABC,
Le point O est le centre du cercle circonscrit au triangle ABC,
![]() Le
point D est le point diamétralement opposé au point B sur ce cercle.
Le
point D est le point diamétralement opposé au point B sur ce cercle.
1. Quelle est la nature du triangle ABD ? Justifier.
2. Quelle est la mesure de l'angle .gif) ? Justifier.
? Justifier.
Problème (12 points)
Dans le jardin de sa nouvelle maison, M. Durand a construit une terrasse rectangulaire qu'il désire recouvrir d'un toit.Pour cela, il réalise le croquis suivant où l'unité de longueur est le mètre.
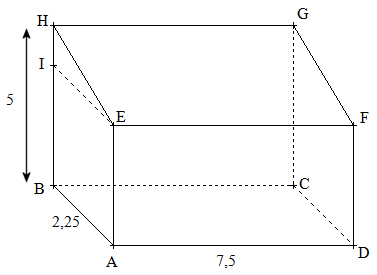
![]() Le
sol ABCD et le toit EFGH sont des rectangles.
Le
sol ABCD et le toit EFGH sont des rectangles. ![]() Le triangle HIE est rectangle
en I.
Le triangle HIE est rectangle
en I. ![]() Le quadrilatère IEAB est un rectangle.
Le quadrilatère IEAB est un rectangle. ![]() La hauteur du sol au sommet du
toit est HB.
La hauteur du sol au sommet du
toit est HB.
On donne : AB = 2,25 ; AD = 7,5 ; HB = 5
Partie I 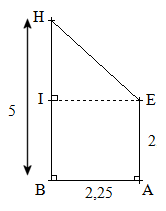
On suppose dans cette partie que AE = 2.
1. Justifier que HI = 3.
2. Démontrer que HE = 3,75.
3. Calculer au degré près la mesure de
l'angle .gif) du
toit avec la maison.
du
toit avec la maison.
Partie II 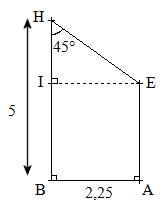
Dans cette partie, on suppose que .gif) et on désire déterminer AE.
et on désire déterminer AE.
1. Quelle est la nature du triangle HIE dans ce cas ? Justifier.
2. En déduire HI puis AE.
Partie III 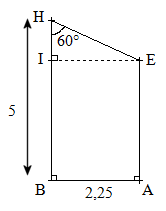
Dans cette partie, on suppose que .gif) et on désire déterminer AE.
et on désire déterminer AE.
1. Déterminer la valeur arrondie au cm de HI.
2. En déduire la valeur arrondie au cm de AE.
Partie IV
La courbe ci-dessous représente la hauteur
AE en fonction de la mesure de l'angle .gif) .
.
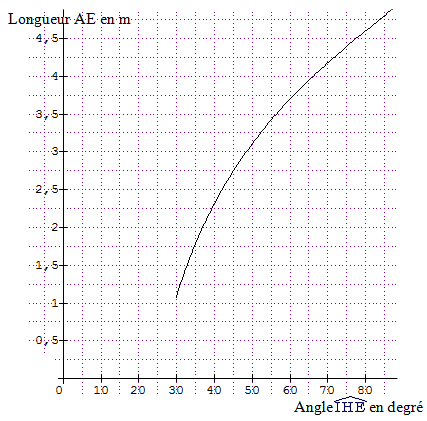
M. Durand souhaite que la hauteur AE soit comprise entre 3 m et 3,5 m. En
utilisant le graphique, donner une mesure possible de l'angle .gif) .
.