BREVET 2007
Activités numériques
 Exercice 1
Exercice 1
1.
Réponse : .gif)
Car :
.gif)
2. Réponse : .gif)
Car : pour
.gif)
.gif)
3. Réponse : .gif)
Car : .gif)
4. Réponse : -10
Car
: pour .gif)
.gif)
5. Réponse : 48 %
Car : En 3e A, sur 30 élèves, il y a 40 % de filles. Il y a donc
: .gif) filles,
soit 12 filles en 3eA.
filles,
soit 12 filles en 3eA.
En 3e B, sur 20 élèves, il y a
60 % de filles. Il y a donc : .gif) filles, soit 12 filles en
3eB.
filles, soit 12 filles en
3eB.
Lorsque les deux classes sont réunies, il y a donc 24 filles
sur un total de 50 élèves. Cela représente .gif) des élèves, soit 48 %.
des élèves, soit 48 %.
lorsque les deux classes sont réunies, il y a 48 % de filles dans le groupe
?
 Exercice 2
Exercice 2
On donne un programme de calcul : 1. Si on fait fonctionner ce programme
avec le nombre -2 :
On lui ajoute 4 : -2 + 4 = 2
On multiplie la somme
obtenue par le nombre choisi (-2) : 2 × (-2) = -4
On ajoute 4 à ce produit :
-4 + 4 = 0
On obtient bien 0 lorsqu'on fait fonctionner ce programme avec le
nombre -2.
2. Lorsque le nombre choisi est 5, on
obtient :
On lui ajoute 4 : 5 + 4 = 9
On multiplie la somme obtenue par
le nombre choisi 5 : 9 × 5 = 45
On ajoute 4 à ce produit : 45 + 4 = 49
On obtient 49 lorsqu'on fait fonctionner ce programme avec le nombre 5.
3. a) Faisons deux autres essais
: ![]() On choisit le nombre 11 :
On choisit le nombre 11 :
On lui ajoute 4 : 11 + 4 = 15
On
multiplie la somme obtenue par le nombre choisi 11 : 15 × 11 = 165
On ajoute
4 à ce produit : 165 + 4 = 169
On obtient 169 lorsqu'on fait fonctionner ce
programme avec le nombre 11.
On peut écrire 169 sous la forme d'un carré :
169 = 13².
On choisit le nombre 8 :
On lui ajoute 4 : 8 + 4 = 12
On multiplie la somme obtenue par le nombre choisi 8 : 12 × 8 = 96
On
ajoute 4 à ce produit : 96 + 4 = 100
On obtient 100 lorsqu'on fait
fonctionner ce programme avec le nombre 8.
On peut écrire 100 sous la forme
d'un carré : 100 = 10².
3. b) Regardons si il en est
toujours ainsi lorsqu'on choisit un nombre entier au départ de ce programme de
calcul :
Choisissons un nombre entier n. On applique le programme
de calcul à ce nombre n :
On lui ajoute 4 : n + 4
On multiplie la somme
obtenue par le nombre choisi n : n(n + 4)
On ajoute 4 à ce produit : n(n +
4) + 4
On obtient n(n + 4) + 4 lorsqu'on fait fonctionner ce programme avec
le nombre n.
Or, n(n + 4) + 4 = n² + 4n + 4 = n² + 2 × n × 2 + 2² = (n +
2)².
Donc : quelque soit le nombre entier choisi au départ, on obtient
toujours un carré comme résultat.
4. Si on souhaite obtenir 1 comme
résultat, il nous faut choisir le nombre entier n tel que : (n + 2)² = 1, donc :
(n + 2)² - 1 = 0
[(n + 2) - 1][(n + 2) + 1] = 0
(n + 1)(n + 3) = 0
Un produit de facteurs est nul si l'un au moins de ses facteurs est nul, et
réciproquement :
| n + 1 = 0 | ou | n + 3 = 0 |
| n = -1 | ou | n = -3 |
Pour obtenir 1 comme résultat, les nombres que l'on peut choisir au départ sont -3 et -1.
Activités géométriques
 Exercice 1
Exercice 1
1. a)
Démontrons que ABC est rectangle en B : On a : AC² = 15² = 225 et AB² + BC² = 9² + 12² = 81 + 144 = 225
Donc AC² = AB² + BC²
D'après la réciproque du théorème de Pythagore, on en conclut que le triangle ABC est rectangle en B.
1. b) 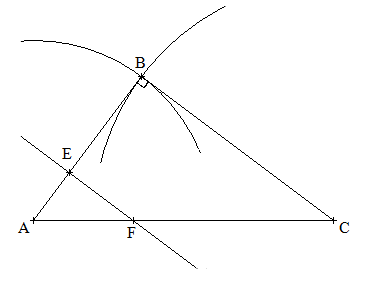
2. a) cf figure
2. b) Démontrons que la droite
(EF) est parallèle à la droite (BC) :
Les points A, E, B sur la
droite (EB) sont dans le même ordre que les points A, F, C sur la droite (FC).
On a : .gif)
Donc .gif) .
.
D'après la réciproque du théorème de Thalès, les droites (EF) et (BC) sont
parallèles.
3. Déterminons EF :
Les droites (EB) et (FC) sont sécantes en A, les droites (EF) et (BC) sont
parallèles. D'après le théorème de Thalès, on a : .gif) , donc
, donc .gif)
De .gif) on en déduit que
on en déduit que .gif)
Donc : EF = 4 cm.
D'autre part, les droites 5EF) et (BA) sonta parallèles et les droites (AB) et (BC) sont perpendiculaires.
"Si deux droites sont parallèles, toute perpendiculaire à l'une est perpendiculaire à l'autre."
Donc (EF) est perpendiculaire à (AB) et le triangle AEF est rectangle en E.
Calculons l'aire du triangle AEF :
.gif)
l'aire du triangle AEF est de
6 cm².
 Exercice 2
Exercice 2
1. Le point A
appartient au cercle de diamètre [BD], donc le triangle ABD est rectangle en A.
2. Mesure de l'angle  :
:
Le triangle ABC est équilatéral, donc 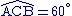
 et
et  sont deux angles inscrits qui
interceptent le même arc
sont deux angles inscrits qui
interceptent le même arc 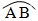 .
Ces deux angles sont donc de même mesure :
.
Ces deux angles sont donc de même mesure : 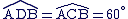
L'angle  mesure 60°.
mesure 60°.
3. Démontrons que les droites
(DC) et (OE) sont perpendiculaires : 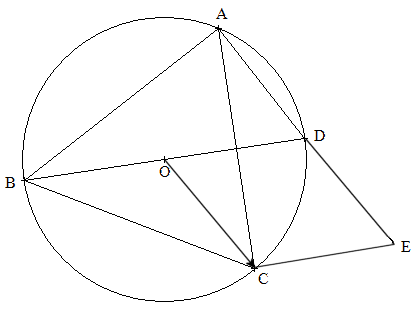
E est l'image du point D par la translation de vecteur .gif) , donc
, donc 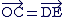 . Le
quadrilatère OCED est donc un parallélogramme.
. Le
quadrilatère OCED est donc un parallélogramme.
De plus, [OC] et [OD] sont
deux rayons du cercle, donc OC = OD.
Le parallélogramme OCED a donc deux
côtés consécutifs de même longueur, c'est donc un losange.
Or, les
diagonales d'un losange se coupent perpendiculairement, donc les droites (DC) et
(OE) sont perpendiculaires.
Problème
Partie IOn suppose dans cette partie que AE = 2.
1. Justifions que HI = 3
:
I est un point du segment [HB], donc HI = HB - IB = 5 - 2 = 3
Donc : HI = 3 m.
2. Démontrons que HE = 3,75
:
Dans le triangle HIE rectangle en I, on applique le théorème de
Pythagore :
HE² = HI² + IE² = 3² + 2,25² = 9 + 5,0625 = 14,0625
Donc :
.gif)
D'où :
HE = 3,75 m.
3. Calculons la mesure de l'angle
.gif) du toit
avec la maison :
du toit
avec la maison :
Dans le triangle IHE rectangle en I, on a :
.gif)
Donc
: 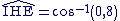
D'où : .gif) au degré près.
au degré près.
Partie II
Dans cette partie, on suppose que .gif) .
.
1. Nature du triangle HIE
:
On sait que le triangle HIE est rectangle en I. De plus, .gif) .
.
Or, la
somme des angles du triangle HIE est égale à 180°, donc l'angle .gif) mesure 45°.
mesure 45°.
On en
conclut que le triangle HIE est rectangle et isocèle en I.
2. Déduisons-en HI :
Le triangle HIE est isocèle en I, donc HI = IE.
Donc : HI = 2,25
m.
Longueur AE :
I est
un point du segment [HB], donc IB = HB - HI = 5 - 2,25
Donc : IB = 2,75 m.
ABIE étant un rectangle, on en conclut que AE = IB.
Donc : AE =
2,75 m.
Partie III
Dans cette partie, on suppose que .gif) .
.
1. Déterminons la valeur arrondie
au cm de HI :
Dans le triangle IHE rectangle en I, on a : .gif)
Donc : .gif)
Donc : 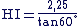
D'où : HI
.gif) 1,30 m
(arrondi au cm près).
1,30 m
(arrondi au cm près).
2. Déduisons-en la valeur
arrondie au cm de AE :
AE = BI = BH - HI .gif) 5 - 1,3
5 - 1,3
Donc AE .gif) 3,70 m (arrondi
au cm près).
3,70 m (arrondi
au cm près).
Partie IV
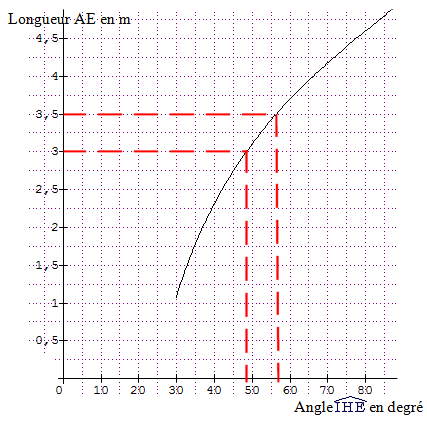
Une mesure possible de l'angle
.gif) est 55°.
est 55°.