Exercice 1 :
                    

1. Calculer A en détaillant les étapes du calcul. Donner le résultat sous forme d'une fraction irréductible.
2. Ecrire B sous forme  où a est un nombre entier. Détailler les étapes du calcul.
3. Calculer C et donner son écriture scientifique en détaillant les étapes du calcul.

Exercice 2 :
Soit D = (2x + 3)² + (2x + 3)(7x — 2)

1. Développer et réduire D.
2. Factoriser D.
3. Calculer D pour x = - 4.
4. Résoudre l'équation (2x + 3)(9x + 1) = 0

Exercice 3 :
Pierre a gagné 84 sucettes et 147 bonbons à un jeu. Etant très généreux, et ayant surtout très peur du dentiste, il décide de les partager avec des amis. Pour ne pas faire de jaloux, chacun doit avoir le même nombre de sucettes et le même nombre de bonbons.

1. Combien de personnes au maximum pourront bénéficier de ces friandises (Pierre étant inclus dans ces personnes !) ? Expliquer votre raisonnement.
2. Combien de sucettes et de bonbons aura alors chaque personne ?

Exercice 4 :
1. Résoudre le système suivant :

2. Une balade d'une heure en mer est proposée à deux groupes de touristes.
Le premier groupe, composé de 8 adultes et de 3 enfants, paie 39,50€. Le second, composé de 7 adultes et de 9 enfants, paie 50,50€.
Quel est donc le prix d'un ticket pour un adulte ? pour un enfant ?

 

II GEOMETRIE

Exercice 1
1. Placer les points A(—3 ; 1), B(—1,5 ; 2,5) et C(3 ; —2) dans le repère orthonormé (O, I, J) de l'annexe 1 ci-jointe.
2. Montrer que.
3. Sachant que et, démontrer que ABC est un triangle rectangle.
4. Placer le point D image de C par la translation de vecteur .
5. Quelle est la nature du quadrilatère ABCD ? Justifier votre réponse.

Exercice 2
Soit un cercle de centre O et de diamètre [ST] tel que ST = 7 cm. Soit U un point de ce cercle tel que SU = 3 cm.

1. Faire une figure.
2. Démontrer que STU est un triangle rectangle en U.
3. Donner la valeur arrondie au dixième de l'angle.
4. En déduire une valeur approchée au dixième de. Justifier votre réponse.

Exercice 3
Sur la figure ci-dessous les mesures ne sont pas respectées.

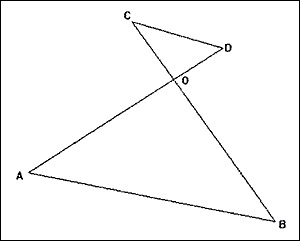
On a  cm,  cm, CO = 3 cm,  est un angle droit et.

1.      Montrer que OB = 9 cm.
2. Montrer que les droites (CD) et (AB) sont parallèles.

 

III PROBLEME

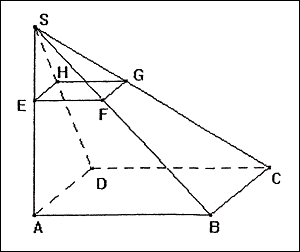
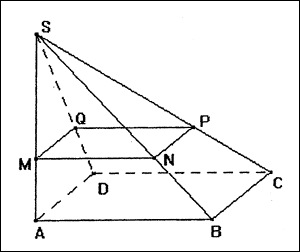
Sur la figure ci-dessous, SABCD est une pyramide à base carrée de hauteur [SA] telle que AB = 9 cm et SA = 12 cm. Le triangle SAB est rectangle en A. Partie A : EFGH est la section de la pyramide SABCD par le plan parallèle à la base et telle que SE = 3 cm. 1. a. Calculer EF. b. Calculer SB. 2. a. Calculer le volume de la pyramide SABCD. b. Donner le coefficient  de réduction permettant de passer de la pyramide SABCD à la pyramide SEFGH. c. En déduire le volume de SEFGH. On donnera une valeur arrondie à l'unité. Partie B : Soit M un point de [SA] tel que SM = x cm, où x est compris entre 0 et 12. On appelle MNPQ la section de la pyramide SABCD par le plan parallèle à la base passant par M. 1. Montrer que MN = 0,75 x. 2. Soit A(x) l'aire du carré MNPQ en fonction de x. Montrer que A(x) = 0,5625 x². 3. Compléter le tableau ci-dessous. 4. Placer dans le repère du papier millimétré de l'annexe 2 les points d'abscisse x et d'ordonnée A(x) données par le tableau. 5. L'aire de MNPQ est-elle proportionnelle à la longueur SM ? Justifier à l'aide du graphique. x : longueur SM en cm 0 2 4 6 8 10 12 A(x) : aire du carré MNPQ               Annexe 2