ENONCE BREVET 2005

I -ACTIVITES NUMERIQUES (12 points)

Exercice 1 :

  1) Calculer A et donner le résultat sous la forme d'une fraction irréductible.
  2) Ecrire B sous la forme 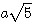où a est un entier relatif.

Exercice 2 :

On donne l'expression  A = (2x-3)²-(4x+7)(2x-3)
  1) Développer et réduire A
  2) Factoriser A
  3) Résoudre l'équation (2x-3) (-2x-10) = 0

Exercice 3 :

Un pâtissier dispose de 411 framboises et de 685 fraises. Afin de préparer des tartelettes, il désire répartir ces fruits en les utilisant tous et en obtenant le maximum de tartelettes identiques.
   1) Calculer le nombre de tartelettes
   2) Calculer le nombre de framboises et de fraises dans chaque tartelette.

Exercice 4 :

Une élève de CP fait des courses pour elle et ses camarades:
- La première fois elle achète 5 crayons et 2 gommes pour 10,90 €
- La deuxième fois elle achète 8 crayons et 3 gommes pour 17,20 €.

En utilisant un système d'équations, aider l'élève de CP à retrouver le prix de chaque article.

II -ACTIVITES GEOMETRIQUES (12 points)

Exercice 1 :

  1) Construire un triangle ABC tel que BC = 7cm ,
        

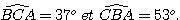
  2) Prouver que ce triangle est un triangle rectangle

  3) Calculer la longueur CA puis donner la valeur arrondie au mm.

Exercice 2 :

  1) Sur la page annexe, à rendre avec la copie, dans le repère orthonormé (O,I,J) tel que OI = OJ = 1cm, placer les points A(0 ; 4)   B(3 ; 2)   C(-1 ; -4).

  2) Calculer la longueur BC, donner la valeur exacte puis la valeur arrondie au dixième.

  3) En admettant que 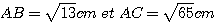, démontrer que le triangle ABC est un triangle rectangle en B.

  4) Placer dans le repère le point E image du point C dans la translation de vecteur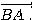  

  5) Démontrer que le quadrilatère ABCE est un rectangle.

Exercice 3 :

  1) Le rayon du disque de base du grand cône est de 7cm. Calculer la valeur exacte du volume du grand cône.

  2) Quel est le coefficient de réduction qui permet de passer du grand cône au plus petit?

  3) Calculer la valeur exacte du volume du petit cône, puis en donner la valeur arrondie au cm³ .

III - PROBLEME (12 points)

Monsieur Martin habite Petitville. Monsieur Gaspard habite à une distance de 900km de Petitville.

A huit heures du matin les deux personnes commencent à rouler l'un vers l'autre:
> Monsieur Martin quitte Petitville et roule à 60km/h
> Monsieur Gaspard se dirige vers Petitville et roule à 90km/h.

On note x le temps écoulé depuis huit heures du matin (x est exprimé en heures). Ainsi, quand il est huit heures du matin, x = 0.

Après avoir roulé une heure, c'est à dire quand x = 1, Monsieur Martin est à 60 km de Petitville et Monsieur Gaspar est lui à 810 km de Petitville.

  1) A quelle distance de Petitville Monsieur MArtin se situe-t-il
         quand x= 4 ?          quand x = 10 ?

  2) A quelle distance de Petitville Monsieur Gaspard se situe-t-il
        quand x = 4 ?     quand x = 10 ?

  3) Exprimer en fonction de x la distance qui sépare Monsieur Martin de Petitville.
      Exprimer en fonction de x la distance qui sépare Monsieur Gaspar de Petitville

  4) On donne les fonctions suivantes:

        .
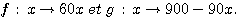 Recopier sur la copie les tableaux suivants et les compléter:

  5) Représenter graphiquement les fonctions f et g sur papier quadrillé en prenant:
         - en abscisse: 1 cm pour une durée d'une heure
         - en ordonnée: 1cm pour une distance de 100km.

  6) A l'aide d'une lecture graphique, déterminer:

        a) La durée au bout de laquelle les deux personnes se croisent
        b) A quelle distance de Petitville se croisent-ils? Faire apparaître les pointillés si nécessaire.

  7) a) Retrouver le résultat de la question 6)a)en résolvant une équation
      b) Retrouver le résultat de la question 6)b) par le calcul.