CORRIGE BREVET 2005
I -ACTIVITES NUMERIQUES (12 points)
Exercice 1 :
1) 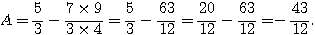
2) 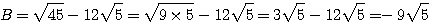
Exercice 2 :
1) A = (2x-3)²-(4x+7) (2x-3) = 4x² -12x + 9 - ( 8x² - 12x +14x - 21 ) = 4x² -12x + 9 - 8x² +12x - 14x + 21 = - 4x² -14x + 30
2) A = ( 2x -3 ) [ ( 2x - 3) - ( 4x +7 )] = ( 2x -3 ) [ 2x - 3 - 4x - 7 ] = ( 2x - 3 ) ( -2x - 10 )
3) ( 2x - 3) ( - 2x - 10 ) = 0
Un produit est nul si et seulement si
un de ses facteurs est nul...
1er cas: 2x - 3 = 0 <=> 2x = 3 <=> x = 3/2 = 1,5
2ème cas:
-2x - 10 = 0 <=> -2x = 10 <=> x = - 10 : 2 = -5
Exercice 3 :
1) Le nombre de tartelettes et le plus grand diviseur commun de 685 et 411.
méthode par soustractions successives:

Le PGCD de 685 et 411 est 137. On peut donc faire 137 tartelettes.
2) 685 : 137 = 5 411 : 137 = 3
On peut donc mettre 5 fraises et 3 framboises par tartelette.
Exercice 4 :
Soit x le prix d'un crayon et y le prix d'une gomme.
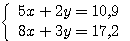 en multipliant la première ligne par
-3 et la deuxième par 2, on obtient le système équivalent:
en multipliant la première ligne par
-3 et la deuxième par 2, on obtient le système équivalent:
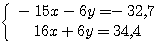 en additionnant les deux égalités membre
à membre, on obtient:
en additionnant les deux égalités membre
à membre, on obtient:
x + 0 = 1,7 ; donc x = 1,7
En remplaçant x par 1,7 dans la première équation on obtient:
5 × 1,7 + 2y = 10,9 soit 8,5 + 2y = 10,9 d'où 2y = 10,9 - 8,5 = 2,4
donc y = 2,4 : 2 = 1,2
Le prix d'un crayon est donc de 1,7 € et le prix d'une gomme est de 1,2 € .
II -ACTIVITES GEOMETRIQUES (12 points)
Exercice 1 :
1)
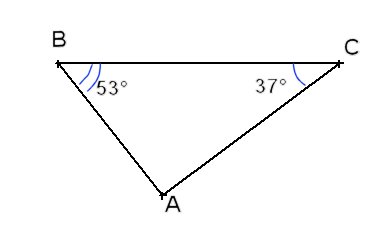
2) La somme des angles d'un triangle fait 180°
Donc  = 180 - ( 53 + 37 ) = 180 - 100 = 90°
Comme  = 90°, le triangle ABC est rectangle en A.
3) Dans le triangle ABC rectangle en A,
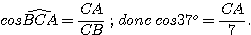

Exercice 2 :
1) Sur la page annexe, à rendre avec la copie, dans le repère orthonormé (O,I,J) tel que OI = OJ = 1cm, placer les points A(0 ; 4) B(3 ; 2) C(-1 ; -4).
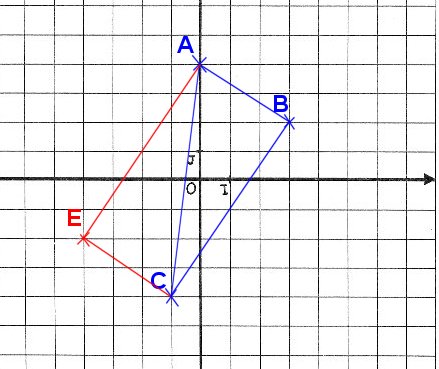
2)

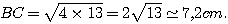
3)
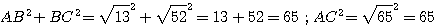
Donc AB²+BC² = AC².
D'après le théorème réciproque de Pythagore, le triangle ABC est rectangle en B.
4) Point E: voir figure
5) E est l'image du point C par la translation de vecteur 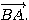
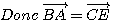 d'où ABCE est
un parallélogramme.
d'où ABCE est
un parallélogramme.
Or ABC est rectangle en B donc ce
parallélograme comprend un angle droit, c'est donc un rectangle.
Exercice 3 :
|
1)
2)
3) Le volume V' du petit cône est donc égal au volume V du grand divisé par 4³ |
|
III - PROBLEME (12 points)
1) distance = vitesse × temps. Appelons d la distance parcourue par M Martin et d' la distance de Monsieur Gaspard à Petitville.
2)
3) Exprimer en fonction de x la distance qui sépare Monsieur
Martin de Petitville: d = 60 x.
Exprimer en fonction
de x la distance qui sépare Monsieur Gaspar de Petitville: d' = 900 - 90
x
4) On donne les fonctions suivantes:
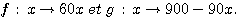 .
.
|
|
5) Représenter graphiquement les fonctions f et g sur papier
quadrillé en prenant:
-
en abscisse: 1 cm pour une durée d'une heure
-
en ordonnée: 1cm pour une distance de 100km.
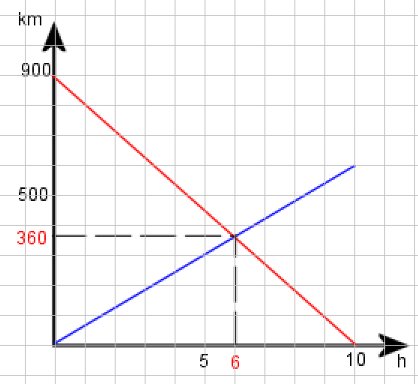
6) A l'aide d'une lecture graphique, déterminer:
a) La durée au bout de laquelle
les deux personnes se croisent: on trouve 6 heures
b)
A quelle distance de Petitville se croisent-ils? on trouve environ 360 km
7) a) Equation: 60x = 900 - 90x
60 x + 90 x = 900 => 150x = 900 => x = 900 : 150 = 6 . On retrouve 6h
b) si x = 6 d = 60 × 6 = 360 . On retrouve 360 km.