PARTIE A
1.
2.
a) 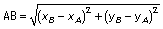
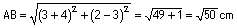
b) Si
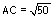 alors
AB = AC
alors
AB = AC
donc le triangle ABC est un triangle isocèle de
sommet A.
3. On a 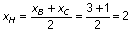
et 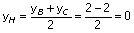
d'où
H (2 ; 0).
4. H est le milieu du segment [BC] donc dans le triangle (ABC), [AH] est la médiane issue de A. Et comme le triangle (ABC) est isocèle de sommet A, alors [AH] est aussi médiatrice et donc hauteur issue de A.
5.
a) (AH) est perpendiculaire à
(BC) donc le triangle (ABH) est rectangle en H donc d'après le théorème de
Pythagore on a
AB2 = AH2 + HB2
or
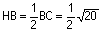
donc on
a 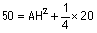
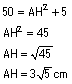
b)
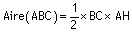
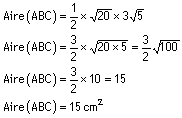
PARTIE B
1. 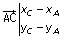
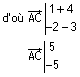
2.
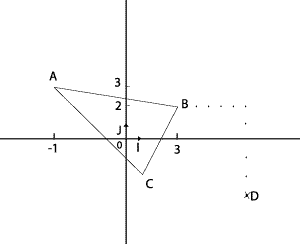
a) Voir graphique
ci-dessus
b) Si D est l'image de B par la translation de vecteur
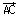 alors on a
alors on a
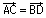
et donc
xD - xB = 5 et
yD - yB = -5
d'où
xD = 5 + xB = 5 + 3 = 8
et
yD = -5 + yB = -5 + 2 = -3
d'où
D (8 ; -3).
3. On a 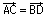 donc le
quadrilatère (ACDB) est un parallélogramme, de plus AB = AC donc
c'est un losange.
donc le
quadrilatère (ACDB) est un parallélogramme, de plus AB = AC donc
c'est un losange.