BREVET 2002 PROBLEME
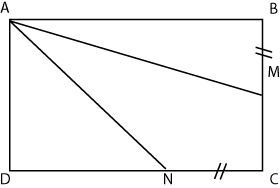
ABCD est un rectangle tel que AB = 6 cm et AD = 4 cm.
Première partie
M est le point du segment [BC] tel que BM = 2 cm.
N est le point du
segment [CD] tel que CN = 2 cm.

1) Calculer AM sous la forme 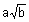 (b nombre entier le plus petit possible).
(b nombre entier le plus petit possible).
2) Démontrer que l'aire du quadrilatère AMCN est de 10 cm2.
Deuxième partie
Les points M et N peuvent se déplacer respectivement sur les segments [BC] et
[CD] de façon que BM = CN = x avec 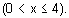
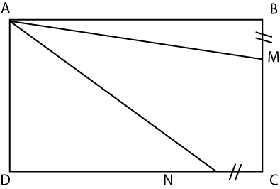
1) Exprimer l'aire du triangle ABM en fonction de x.
2) a) Calculer DN en fonction de x.
b)
Démontrer que l'aire du triangle ADN en fonction de x est 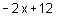 .
.
3) a) Dans un repère orthonormé (O, I, J) avec OI = OJ = 1 cm, représenter
graphiquement les fonctions affines :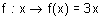 et g : x
et g : x 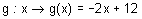
b) Calculer les coordonnées du
point R intersection de ces deux représentations.
4) a) Pour quelle valeur de x les aires des triangles ABM et ADN sont-elles
égales ?
Justifier la réponse.
b) Pour cette
valeur de x, calculer l'aire du quadrilatère AMCN.