
Le cube, le pavé droit
1°) Le cube
|
La figure ci-contre est un cube. |
|
Le cube comprend donc 6 faces, 8 sommets et 12 arêtes.
Les faces opposées sont parallèles.
Toutes les arêtes sont de même longueur:
AB = DC = EF = HG = AD = BC = EH = GF = AE = BF = DH = CG..
Parallélisme
des arêtes: (AB) // (EF) // (DC) // (GH); (AD) // (BC) // (FG) // (EH); (AE)
// (BF) // (DH) // (CG).
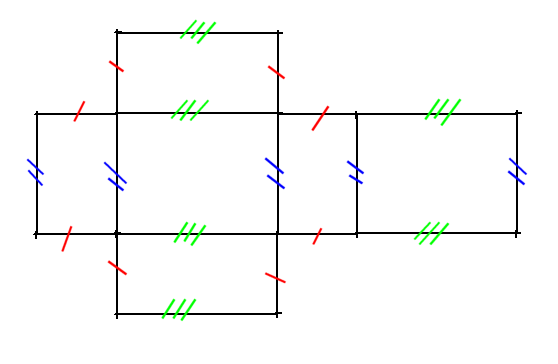
Patron d'un cube:

Calcul du volume: si on pose c le côté ( c'est à dire la longueur de l'arête) V = c × c × c
Exemple: un cube de côté 7cm; son volume est de : V = 7 × 7 × 7 = 343 cm³
L'unité de volume est ici le cm³
2°) Pavé droit
|
La figure ci-contre est un pavé droit, Il comporte comme le cube: Il est caractérisé par 3 dimensions: |
|
On retrouve le même parallélisme des faces et des arêtes que pour le cube.
Patron d'un pavé droit:
Calcul du volume: V = L × l × h
Exemple: si L = 8cm; l = 5cm et h = 4cm, alors V = 8 × 5 × 4 = 160 cm³.
3°) Unités de volume:
L'unité de base des volumes est le mètre cube: m³. 1 m³ représente donc un
cube de 1m de côté.
Or 1m = 10 dm. Si on mesure le même cube en dm³, on trouve
alors un volume de 10×10×10 = 1000 dm³ !
Donc 1m³ = 1000 dm³ . Cela
explique pourquoi on doit mettre 3 chiffres par colonne dans un tableau
de conversion.
D'autre part, pour mesurer les capacités, il est d'usage de d'exprimer les
résultats en litres.
Or: 1L = 10 dL = 100 cL = 1000 mL. Enfin, un
cube 10cm de côté fait exactement un volume de 1L
Donc 1L = 1dm³. Exemple
de tableau:
|
m³ |
dm³ |
cm³ |
mm³ |
||||||||
|
|
|
|
hL |
daL |
L |
dL |
cL |
mL |
|
|
|
|
|
|
2 |
8 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
5 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
7 |
8 |
0 |
0 |
|
|
|
Exemples: 2,8 m³ = 2800L ; 15L = 15000cm³ ; 7800cm³ = 7,8L
4°) Exercices:
a) Calculer le volume d'un cube de côté 8cm
Réponse:
b) Calculer le volume d'un parallélépipède rectangle de dimensions 12cm; 9cm; 6cm.
Réponse:
c) Convertir en litres: 2,7m³ =
Réponse:
d) Convertir en cm³: 4,5L =
Réponse:
© J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.