
Le théorème de Thalès dans le triangle
|
Si dans un triangle ABC, le point B' est sur [AB], le point C' est sur [AC ] et si (B'C') est parallèle à (BC), alors on a l'égalité:
|
|
Exemple:
On donne: AB = 5,5cm; AC = 6cm; BC = 3,5cm.
On place B' sur [AB] tel que AB'= 4,4cm .
La parallèle à (BC ) passant par B' coupe [AC] en C'.
Calculez AC' et B'C'.
Solution: Dans le triangle ABC:
le point B' est sur [AB], le point C' est sur [AC] et (B'C') est parallèle à (BC).
d'après le théorème de Thalès:
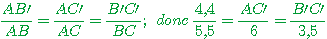
En utilisant les produits en croix:
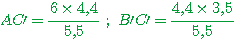
donc AC'=4,8cm et B'C'= 2,8cm
Construction: partage d'un segment en plusieurs segments égaux
Exercice :
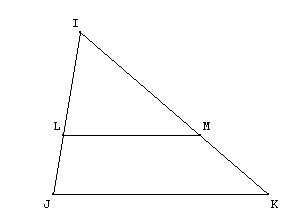
IJK est un triangle tel que IJ = 3,6cm; IK = 4,8cm.
(LM) est parallèle à (JK) et on donne IL = 3cm et LM = 2,5cm.
Question 1. Calculez IM :
Question 2. Calculez JK:
© J-P Diérick, professeur certifié de Mathématiques, collège du Triolo.