ECRITURES FRACTIONNAIRES

1°) Généralités

Si b ¹ 0 , 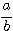représente une écriture fractionnaire de numérateur a et de dénominateur b.

Si a et b sont des nombres entiers (avec b¹ 0), alors 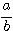est une fraction

On peut utiliser des entiers relatifs:

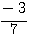est une fraction

Remarque: on évitera d'écrire 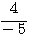, on écrira plutôt

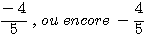
a) Partage:

Une fraction représente un partage...

Par exemple, la partie coloriée en rouge représente les 3/8 du disque.

b) Fractions décimales:

Une fraction peut aussi être considérée comme le résultat d'une division

Cela peut être un nombre décimal ( exemple 3/4 = 3:4 = 0,75 ) ou non (2/3 = 2:3 = 0,6666... ce n'est pas un nombre décimal)

Les fractions qui représentent un nombre décimal sont appelées fractions décimales ( exemple: 53/100 ; 3/10; 37/1000 ...).

Un nombre décimal peut toujours s'écrire sous forme de fraction décimale: 0,7 = 7/10 ; 0,083 = 83 / 1000 ; 5,29 = 529 / 100...

c) fractions égales

Une fraction peut avoir beacoup d'écritures différentes: 3/5 = 6/10 = 9 / 15 ...

C'est une conséquence de la propriété :

"On ne change une fraction si on multiplie (ou divise) le numérateur et le dénominateur par un même nombre."

si b et k sont non nuls, alors : 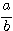= 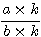. Cette propriété est utile pour simplifier ou pour mettre des fractions au même dénominateur.

Exemple, simplifier :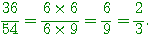

2°) Somme et différence

-Pour additionner ou soustraire deux fractions, il faut d’abord le mettre au même dénominateur

puis on additionne ou soustrait les numérateurs et on garde le dénominateur commun

Exemples :

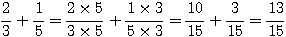
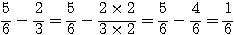
4°) Produit

-Pour multiplier deux fractions, on multiplie entre eux les numérateurs et on multiplie entre eux les dénominateurs

Exemples :

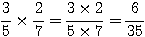
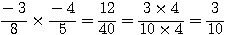
5°) Fraction d’une quantité

Exemple : prendre les 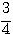de douze Euros, c’est multiplier 12 par 3 et diviser par 4:

€

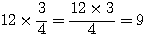6°) Inverse et quotient

L’inverse de 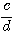est 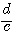. Diviser par 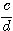, c’est multiplier par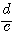

Exemples :

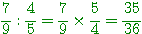
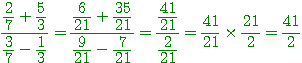
6°) Produits en croix

Pour trouver le terme manquant dans l'égalité de deux fractions (ou dans une proportion) ,

on utilise les "produits en croix".

Exemple:

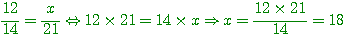
7°) Exercices:

Exercice 1. Calculez:

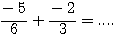. (donnez une réponse simplifiée de la forme a/b)

Exercice 2:

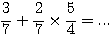
Exercice 3:

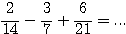
Exercice 4:

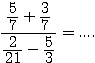
Exercices supplémentaires (avec l'aimable autorisation de Franck Jarnier)